Внутренняя энергия и работа газа.
1. Понятие – внутренняя энергия
Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно-кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно-кинетические модели для иллюстрации своих выводов.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамической равновесной системы является выравнивание температуры всех ее частей.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом.
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел.
Что такое внутренняя энергия?
Когда скользящая по льду шайба останавливается под действием силы трения, то ее механическая (кинетическая) энергия не просто исчезает, а передается беспорядочно движущимся молекулам льда и шайбы. Неровности поверхностей трущихся тел деформируются при движении, и интенсивность беспорядочного движения молекул возрастает. Оба тела нагреваются, что и означает увеличение их внутренней энергии.
Нетрудно наблюдать и обратный переход внутренней энергии в механическую. Если нагревать воду в пробирке, закрытой пробкой, то внутренняя энергия воды и внутренняя энергия пара начнут возрастать. Давление пара увеличится настолько, что пробка будет выбита. Кинетическая энергия пробки увеличится за счет внутренней энергии пара. Расширяясь, водяной пар совершает работу и охлаждается. Его внутренняя энергия при этом уменьшается.
2. Внутренняя энергия как сумма кинетической и потенциальной энергии тела
С точки зрения молекулярно-кинетической теории внутренняя энергия макроскопического тела равна сумме кинетических энергий беспорядочного движения всех молекул (или атомов) тела и потенциальных энергий взаимодействия всех молекул друг с другом (но не с молекулами других тел).
Вычислить внутреннюю энергию тела (или ее изменение), учитывая движение отдельных молекул и их положения относительно друг друга, практически невозможно из-за огромного числа молекул в макроскопических телах. Поэтому необходимо уметь определять значение внутренней энергии (или ее изменение) в зависимости от макроскопических параметров, которые можно непосредственно измерить.
3. Внутренняя энергия идеального одноатомного газа.
Наиболее прост по своим свойствам одноатомный газ, состоящий из отдельных атомов, а не молекул. Одноатомными являются инертные газы — гелий, неон, аргон и др. Вычислим внутреннюю энергию идеального одноатомного газа.
С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом.
U = Eкин + Епот.
Так как взаимодействие между молекулами идеального газа практически отсутствует, то потенциальная энергия их взаимодействия равна нулю.
Епот = 0
Тогда U = Eкин.
Для N числа молекул последняя формула перепишется виде:
U = NEкин. (1)
Число молекул в веществе равно:
(2)
Средняя кинетическая энергия теплового движения молекул равна:
(3)
Подставляя формулы (2) и (3) в формулу (1), получаем:
Произведение NAκ = R, где R – универсальная газовая постоянная.
Тогда внутренняя энергия идеального одноатомного газа равна:
(5)
Как видно из формулы (5) внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема.
4. Обобщенная формула для вычисления внутренней энергии газа
В
общем случае ,
где i – число степеней свободы
i = 3 для одноатомного газа
i =5 для двухатомного газа
i =6 для многоатомного газа
Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния.
Изменение внутренней энергией определяется формулой (6):
.
5. Работа в термодинамике
Понятие – работа в термодинамике
В результате каких процессов может меняться внутренняя энергия? Есть два вида таких процессов: совершение работы и теплопередача. Начнем с работы. Чему она равна при сжатии и расширении газа и других тел?
В механике работа определяется как произведение модуля силы, модуля перемещения точки ее приложения и косинуса угла между ними. При действии силы на движущееся тело работа равна изменению его кинетической энергии.
В термодинамике движение тела как целого не рассматривается, речь идет о перемещении частей макроскопического тела друг относительно друга. В результате может меняться объем тела, а его скорость остается равной нулю.
Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии.
Почему при сжатии или расширении тела меняется его внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?
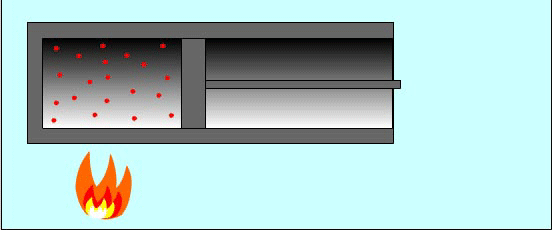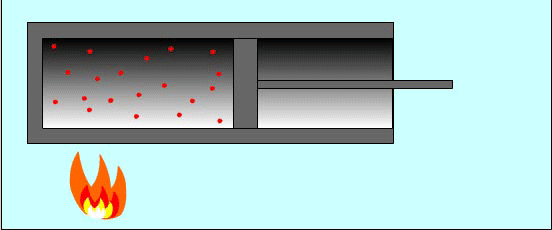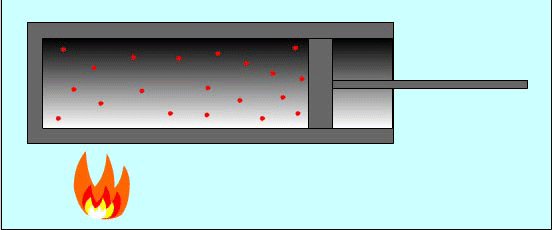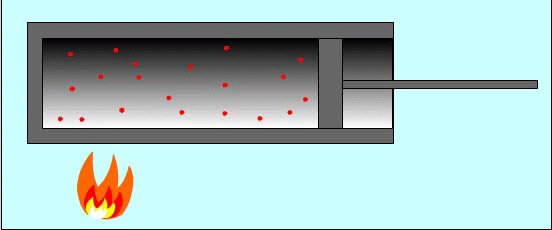
Причина изменения температуры газа в процессе его сжатия состоит в следующем: при упругих соударениях молекул газа с движущимся поршнем изменяется их кинетическая энергия. Так, при движении навстречу молекулам газа поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги. Нога сообщает мячу скорость, значительно большую той, которой он обладал до удара.
И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, — нога футболиста движется от мяча, как бы уступая ему дорогу.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
6. Вычисление работы.
Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем. Проще всего вначале вычислить не работу силы F, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой F'.
Согласно третьему закону Ньютона F = - F'. Модуль силы, действующей со стороны газа на поршень, равен F' = pS, где р — давление газа, a S — площадь поверхности поршня. Пусть газ расширяется изобарно и поршень смещается в направлении силы F' на малое расстояние Δh = h2 – h1. Так как давление газа постоянно, то работа газа равна:
А' = F'Δh = pS (h2 -h1)=p (Sh2 – Sh1).
Эту работу можно выразить через изменение объема газа.
Начальный его объем V1 = Sh1, а конечный V2 = Sh2.
Поэтому А' = р (V2 – V1) = pΔV (1),
где ΔV = V2 – V1.
При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают.
Если газ сжимается, то формула (1) для работы газа остается справедливой. Но теперь V2 < V1 и поэтому А' < О.
Работа А, совершаемая внешними телами над газом, отличается от работы самого газа А' только знаком: А = -А', так как сила F, действующая на газ, направлена против силы F', а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна: А = -А' = -рΔV
7. Геометрическое истолкование работы. Работе А' газа для случая постоянного давления можно дать простое геометрическое истолкование.
Построим график зависимости давления газа от занимаемого им объема (рис. 1). Здесь площадь прямоугольника abdc, ограниченная графиком р = const, осью V и отрезками аb и cd, равными давлению газа, численно равна работе:
A'=P1 (V2 – V1) = |аb | · |ас|.
Рисунок 1 Рисунок 2
В общем случае давление газа не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 2). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости р от V, осью V и отрезками аb и cd, равными давлениям р1, р2 в начальном и конечном состояниях газа.
Таким образом, работа, совершаемая газом а процессе его расширения (или сжатия) при любом термодинамическом процессе, численно равна площади под кривой, изображающей изменение состояния газа на диаграмме (р,V).
Основные формулы для определения работы газа
Работа газа при изобарном процессе A/ = p·Δ V
i – число степеней свободы
i =3, для одноатомного газа
i =5, для двухатомного газа
i =6, для многоатомного газа
Работа газа при изохорном процессе А/ = 0
Работа, совершенная над газом А = - А/
Примеры решения задач:
Задача 1. На сколько изменяется внутренняя энергия гелия массой 200 г при увеличении температуры на 20 °С?
Задача 2. При уменьшении объема одноатомного газа в 3,6 раза его давление увеличилось на 20%. Во сколько раз изменилась внутренняя энергия?
Задача 4. В вертикально расположенном цилиндре с площадью основания 1 дм2 под поршнем массой 10 кг, скользящим без трения, находится воздух. При изобарном нагревании воздуха поршень поднялся на 20 см. Какую работу совершил воздух, если наружное давление равно 100 кПа?
Задача 5. Температура воздуха в комнате объемом 70 м3 была 280 К. После того как протопили печь, температура поднялась до 296 К. Найти работу воздуха при расширении, если давление постоянно и равно 100 кПа.
Задачи на расчет работы газа
1. Какая работа А совершается при изотермическом расширении водорода массой m=5 г, взятого при температуре T=290 К, если объем газа увеличивается в три раза?
2. В двух цилиндрах под подвижным поршнем находятся водород и кислород. Сравнить работы, которые совершают эти газы при изобарном нагревании, если их массы, а также начальные и конечные температуры равны.
3. Воздух массой 15 кг нагрели от температуры 100оС до температуры 250оС при постоянном давлении. Чему равна работа при расширении воздуха и изменение его внутренней энергии?
4 Идеальный газ нагрели на 20 К при постоянном давлении, и он совершил работу, равную 249 кДж. Чему равно количество вещества газа, который нагрели?
5. При изобарном нагревании гелия массой 12 г он совершил работу, равную 1 кДж. На сколько изменилась температура газа и какое количество теплоты ему было передано?
Задачи на расчет внутренней энергии газа
1. На сколько изменяется внутренняя энергия гелия массой 100 г при увеличении температуры на 40 °С?
2. Сравнить внутренние энергии аргона и гелия при одинаковой температуре. Массы газов одинаковы.
3. Какова внутренняя энергия гелия, заполняющего аэростат объемом 60 м3 при давлении 100 кПа?
4. При уменьшении объема одноатомного газа в 2 раза его давление увеличилось в 1,5 раза. Во сколько раз изменилась внутренняя энергия?
5. Сравнить внутреннюю энергию газа, находящегося в открытой колбе, до нагревания с внутренней энергией газа, оставшегося в колбе после изобарного нагревания.
Домашнее задание:
Контрольные вопросы:
1. Приведите примеры превращения механической энергии во внутреннюю и обратно в технике и быту.
2. От каких физических величин зависит внутренняя энергия тела?
3. Чему равна внутренняя энергия идеального одноатомного газа?
4. Почему газы при сжатии нагреваются?
5. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображенном на рисунке 2?
Задачи:
1. Азот массой 280 г был нагрет при постоянном давлении на 100 К. Чему равна работа, которую совершил газ при расширении?
2. Газ, изобарно расширяясь при давлении 2×105 Па, совершает работу 200 Дж. Чему равен первоначальный объем газа, если его конечный объем оказался равным 2,5 л?
3. Чему равна работа, которую совершает воздух, изобарно расширяясь при давлении 2×105 Па, когда его нагревают на 17оС? Первоначальный объем воздуха был равен 15 м3, а температура – 0оС.
4. При изобарном нагревании идеального газа его объем увеличился в 3 раза при давлении 3×105 Па. Чему был равен первоначальный объем газа, если для его увеличения потребовалось совершить работу 12,9 кДж?
5. Как изменяется внутренняя энергия газа при изобарном нагревании? Изохорном? Изотермическом?
6. Какова внутренняя энергия 10 моль одноатомного газа при 270С?