2. Основные понятия и определения термодинамики.
Совокупность макроскопических тел, которые при взаимодействии обмениваются энергией между собой и окружающей средой, называют термодинамической системой.
Взаимодействие в физике – воздействие тел или частиц друг на друга, приводящее к изменению состояния их движения.
Физические величины (например, давление, температура и т. д.), характеризующие состояние термодинамической системы в данный момент времени, называют параметрами состояния, или термодинамическими параметрами.
Число независимых параметров состояния равно числу степеней свободы термодинамической системы.
Различают параметры состояния физической системы экстенсивные, т. е. пропорциональные массе системы (объем, внутренняя энергия, свободная энергия, энтропия, термодинамические потенциалы и другим видам энергий), и интенсивные, независящие от массы (давление, температура и прочие).
Рассмотрим некоторые из них.
1) Давление – физическая величина, характеризующая интенсивность сил, с которыми одно тело действует нормально (перпендикулярно) на поверхность другого – внутренний параметр системы.
При равномерном распределении силы по поверхности давление находится по формуле:
В СИ единицей измерения давления считается паскаль (Па), 1 Н/м2 = 1 Па.
На практике традиционно используют некоторые внесистемные единицы.
Например, 1 бар = 105 10×Па, 1 ат = 9,81× 104 Па (техническая атмосфера), 1 мм рт. ст.= 1,33× 102Па, 1атм =1,033 ат =105 Па (нормальная атмосфера).
Для измерения давления используют манометры, барометры, вакуумметры, а также различные датчики давления.
Виды измеряемого давления:
1. Барометрическое (атмосферное) В - давление, измеряемое барометрами.
2. Манометрическое (превышающее атмосферное)
Давление газа в сосуде называется абсолютным (Рабс или Ра). Превышение давления в сосуде над барометрическим называется избыточным (Ризб или Ри).
Уравнение равновесия Ра = В + Ри
Превышение барометрического давления над давлением в сосуде называется разрежением (Рр).
Уравнение равновесия по сечению АС следующее Ра = В - Рр
2. Температура
Температура – физическая величина, характеризующая состояние термодинамического равновесия для всех частей макроскопической системы и являющаяся мерой отклонения от этого равновесия.
Температура – функция состояния системы, не зависит от предыстории термодинамической системы (нулевое начало термодинамики).
Температуру невозможно измерить непосредственно.
Для измерения температуры используют температурные шкалы. Например, газовая и термодинамическая температурная шкалы.
Термодинамическая температурная шкала основана на выводах второго начала термодинамики.
Абсолютная температура по термодинамической температурной шкале обозначается символом Т, в СИ измеряется в кельвинах (К).
Для термодинамической температурной шкалы, как и для любой другой, необходимо задать значения двух фиксированных температур.
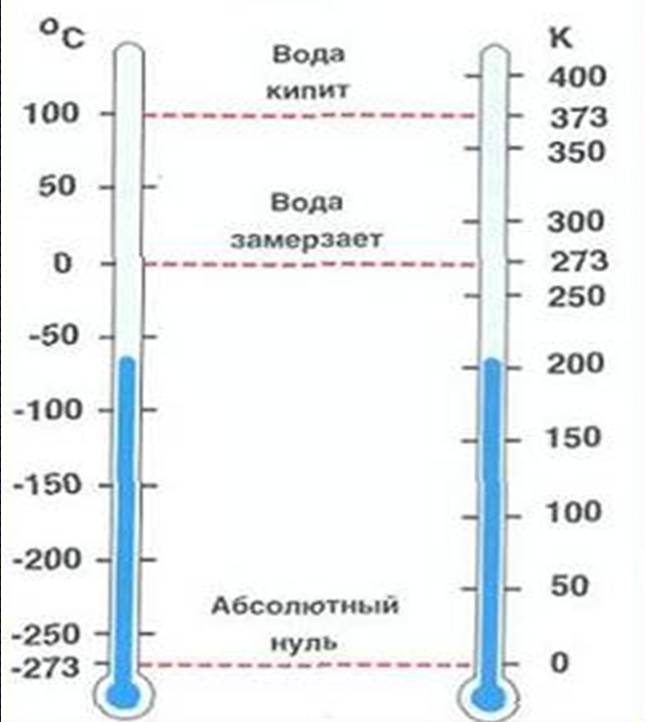
Например, Т = 0 К (абсолютный нуль температуры) и Т = 273,15 К (точка плавления льда при нормальном давлении). На рис. 1.1 приведены некоторые температурные шкалы. Введение Т = 0 К является экстраполяцией и не требует реализации абсолютного нуля.
Термодинамическая (абсолютная) температурная шкала (шкала Кельвина) имеет единицы температуры, совпадающие с единицами температуры для стоградусной шкалы Цельсия, основанной на свойствах идеального газа и значениях t = 0 oC (точка плавления льда) и t = 100 oC (точка кипения воды).
Соотношение между температурами по шкале Цельсия и шкале Кельвина записывают в виде: Т = t oC + 273,15 oC.
На практике для измерения температуры используют термометры, градуированные по высокостабильным реперным точкам, таким, как тройная точка кислорода, водорода, аргона; точки кипения этих и других газов (например, неона); точки затвердевания чистых металлов и т. д., температуры которых по термодинамической температурной шкале найдены предельно точными измерениями.
Температура – мера средней кинетической энергии молекул.
Основное
уравнение МКТ имеет вид:
,
учитывая, что n = N/V, получим:
.
Измерив
отношение ,
для трех веществ: водорода, гелия, кислорода получили, что данное отношение
имеет одинаковые значения в независимости от вещества. Оно изменяется только с
изменением температуры. Величина
Q
растет с повышением температуры.
Q = κ Т, где κ – коэффициент пропорциональности.
(1),
где κ = 1,38*10-23 Дж/К – постоянная Больцмана.
Постоянная Больцмана связывает температуру Q в энергетических единицах с температурой в Кельвинах.
Учитывая, что
.
Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.
Чем выше температура, тем быстрее двигаются молекулы.
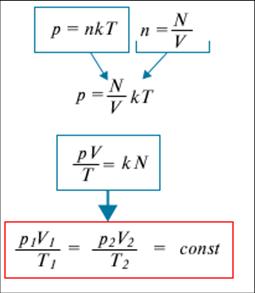
Так как n = N/V, получим Р = n κ Т.
2. Давление идеального газа. Уравнение Менделеева-Клайперона.
Вывод уравнения Менделеева-Клайперона:
Произведение постоянной Больцмана к и постоянной Авогадро Na называют универсальной (молярной) газовой постоянной и обозначают буквой R:
R = kNA = 1,38 • 10 23 Дж/К • 6,02 • 1023 1/моль = 8,31 Дж*моль • К).
Уравнение состояния в форме (1) было впервые получено великим русским ученым Д. И. Менделеевым.
Его называют уравнением Менделеева — Клапейрона.
или
Для чего нужно уравнение состояния? Не только идеальный газ, но и любая реальная система — газ, жидкость, твердое тело — характеризуется своим уравнением состояния. Но только эти уравнения намного сложнее, чем уравнение Менделеева — Клапейрона для идеального (достаточно разреженного) газа.
Практическое применение уравнения Менделеева-Клайперона.
Знать уравнение состояния необходимо при исследовании тепловых явлений. Оно позволяет полностью или частично ответить сразу на три группы различных вопросов.
1. Уравнение состояния позволяет определить одну из величин, характеризующих состояние, например температуру, если известны две другие величины. Это и используют в термометрах.
2. В газовых законах. Зная уравнение состояния, можно сказать, как протекают в системе различные процессы при определенных внешних условиях: например, как будет меняться давление газа, если увеличивать его объем при неизменной температуре, и т. д.
3. В молекулярной физике. Наконец, зная уравнение состояния, можно определить, как меняется состояние системы, если она совершает работу или получает теплоту от окружающих тел.
Уравнение Клайперона
Получим другую форму записи уравнения состояния, называемое уравнением Клапейрона.
3. Понятие термодинамический процесс
Состояние макроскопической системы определяется большим числом параметров, и установление равновесия по каждому из параметров протекает по-разному.
Состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени, в условиях изоляции от окружающей среды, называют равновесным.
Состояние термодинамической системы, в котором хотя бы один из параметров, характеризующих ее состояние, изменяется, называют неравновесным.
В состоянии термодинамического равновесия параметры системы не меняются с течением времени во всех ее точках и прекращаются все необратимые процессы, связанные с диссипацией энергии.
Определяющей величиной вещества
(газообразного, жидкого, твердого) является соотношение между средней
кинетической энергией и средней потенциальной энергией молекул этого вещества,
т. е.
Для газовой фазы e (Т, Р) << 1,
жидкой фазы e(Т, Р) » 1
твердой фазы e (Т, Р) >>1.
Если термодинамическую систему, находящуюся в неравновесном состоянии, изолировать от окружающей среды и предоставить самой себе, то она перейдет самопроизвольно в равновесное состояние.
Переход термодинамической системы из одного состояния в другое называют термодинамическим процессом.
Процесс перехода системы от неравновесного состояния к равновесному называют релаксацией.
Количественной мерой релаксации служит время релаксации.
Например, приближение к состоянию равновесия кристаллических структур в земной коре длится геологические эпохи (миллионы и миллиарды лет).
Все релаксационные процессы являются неравновесными.
Примерами термодинамических процессов являются:
1. Изохорический процесс (V = const) – процесс перехода термодинамической системы из одного состояния в другое при постоянном объеме – закон Шарля.
2. Изобарический процесс (Р = const) – процесс перехода термодинамической системы из одного состояния в другое при постоянном давлении – закон Гей-Люссака.
3. Изотермический процесс (T = const) – процесс перехода термодина- мической системы из одного состояния в другое при постоянной температуре – закон Бойля – Мариотта.
4. Адиабатический процесс (Q = const) – процесс перехода термодинамической системы из одного состояния в другое без теплообмена с окружающей средой – закон Пуассона.
4. Изопроцессы в газах
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.
Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.
1) Изобарный процесс. Закон Гей-Люссака.
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческого слова «барос» — вес).
Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.
Этот закон был установлен экспериментально в 1802 г. французским
ученым Ж.
Гей-Люссаком
(1778—1850) и носит название
закона
Гей-Люссака.
при
Р = const
Из закона Гей-Люссака следует, что при постоянном давлении газа его объем прямо пропорционален температуре. Для двух состояний газа можно записать выражение
.
При увеличении температуры газа в 4 раза, его объем увеличится тоже в 4 раза.
Графически изобарный процесс изображается прямой, которая называется изобарой. Различным давлениям соответствуют разные изобары. Изобара соответствующая более высокому давлению, лежит ниже изобары, соответствующей более низкому давлению.
В области низких температур все изобары идеального газа сходятся в точке Т = 0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может
Данный закон приближенно можно наблюдать, когда происходит расширение газа при его нагревании в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня. Другим проявлением закона Гей-Люссака в действии является аэростат.
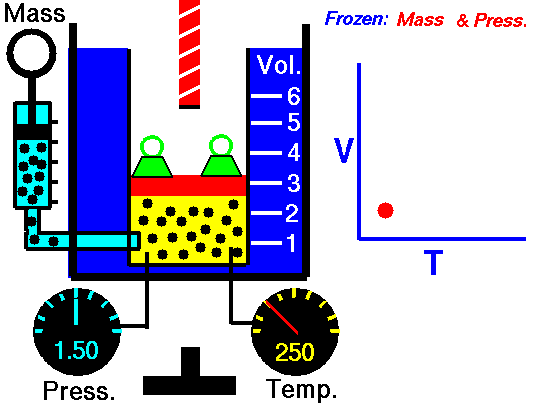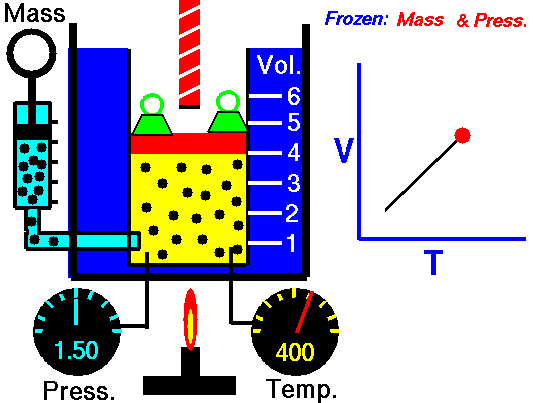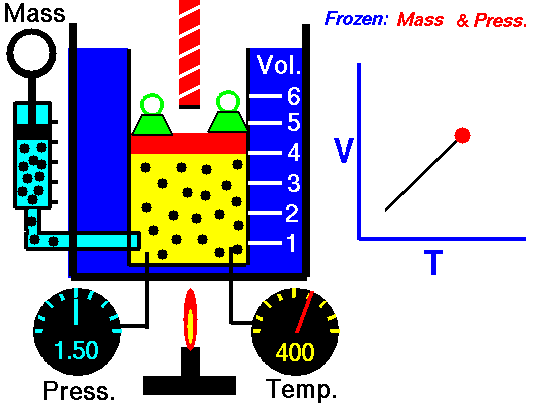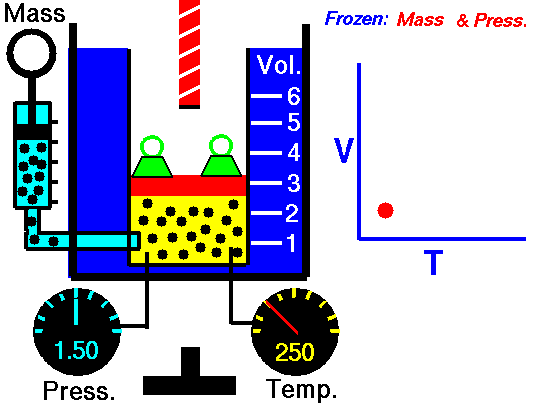
Закон справедлив при температурах, далеких то абсолютного нуля, и малых значениях плотности уравнение может быть использовано для описания свойств любых газов
2) Изохорный процесс. Закон Шарля.
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (от греческого слова «хорема» — вместимость).
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Этот газовый закон был установлен в 1787 г. французским физиком Ж. Шарлем (1746—1823) и носит название закона Шарля.
при V = const
Для двух состояний
газа можно записать выражение
.
Эта зависимость изображается прямой, называемой изохорой. Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля — Мариотта падает. Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
Все изохоры идеального газа начинаются в точке Т = 0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Данный закон приближенно можно наблюдать, когда происходит увеличение давления газа в любой емкости или в электрической лампочке при нагревании.
Изохорный процесс используется в газовых термометрах постоянного объема.
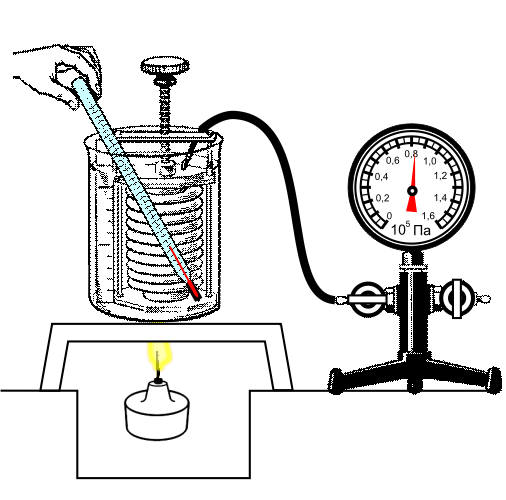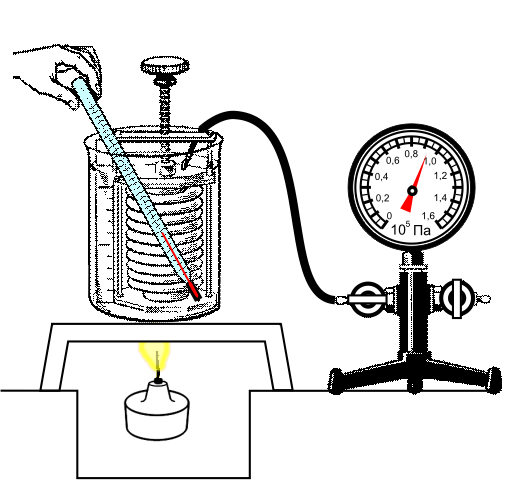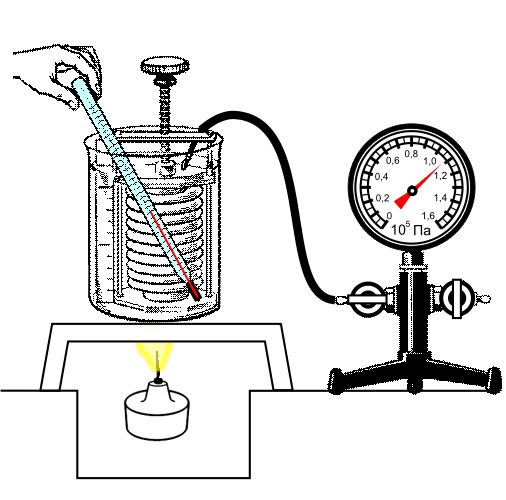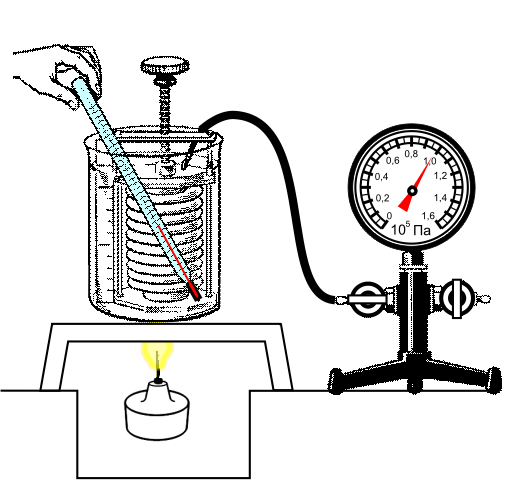
Любой баллон, предназначенный для хранения газа, имеет свой запас прочности, максимальное давление, которое он может выдержать. Давление, как описывает закон Шарля, зависит от температуры. Практически можно рассчитать для каждого баллона температуру, до которой этот самый баллон можно нагревать.
Закон Шарля не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
3) Изотермический процесс. Закон Бойля-Мариотта.
Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим.
pV = const при Т = const.
Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Для двух состояний газа можно записать выражение p1 V1 = p2 V2 .
При увеличении объема газа в 2 раза его давление уменьшается тоже в 2 раза.
Закон Бойля-Мариотта открыт в 1662 английским ученым Робертом Бойлем. В 1676 году, независимо от выводов Р. Бойля, закон был описан французским физиком Эдмом Мариоттом, поэтому носит двойное название по фамилиям авторов.
Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой.
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т2, лежит выше изотермы, соответствующей более низкой температуре Т1.
Закон может быть использован для описания свойств газа в природе или технике при постоянной температуре.
Применение закона: в технике приближенно можно наблюдать в процессе сжатия воздуха компрессором или в результате расширения газа под поршнем насоса при откачке его из сосуда.
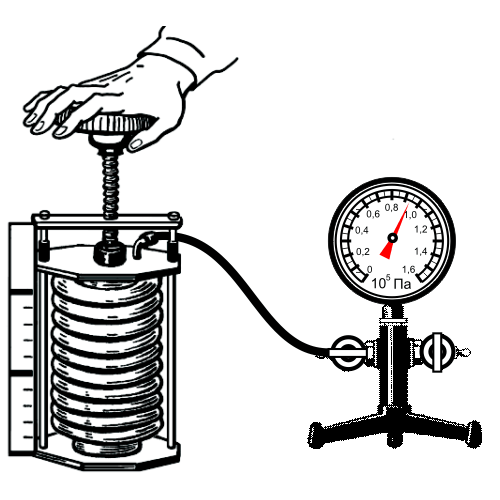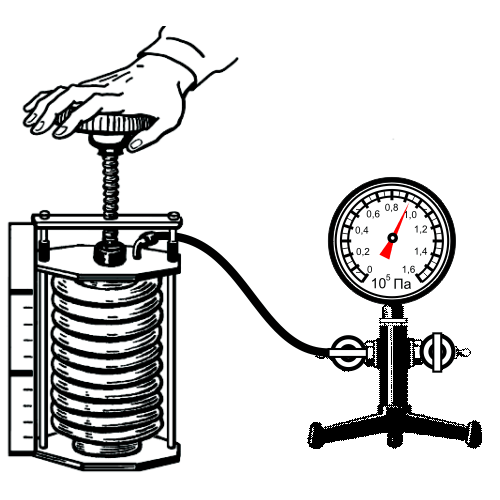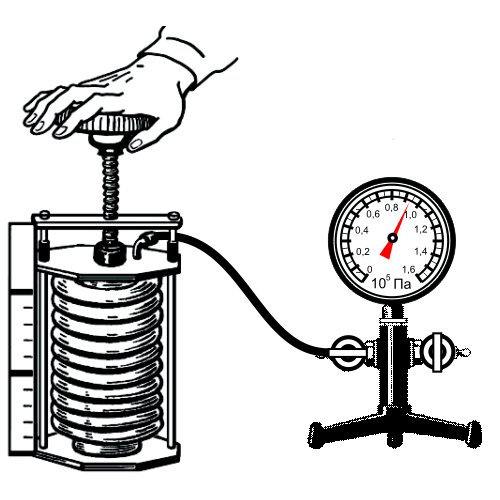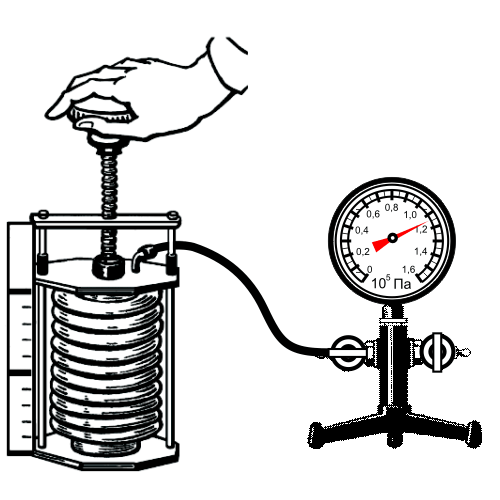

Примеры решения задач:
Задача 1. Каково давление газа, если средняя квадратическая скорость его молекул 500 м/с, а его плотность 1,35 кг/м3?
Задача 2. В результате нагревания давление газа в закрытом сосуде увеличилось в 4 раза. Во сколько раз изменилась средняя квадратическая скорость?
Задача 3. Во сколько раз изменится давление газа при увеличении его объема в 2 раза? Средняя скорость движения молекул осталась неизменной.
Задача 4. Современные вакуумные насосы позволяют понижать давление до 1,3·10-10 Па. Сколько молекул газа содержится в 1см3 при указанном давлении и температуре 270С.
Задача 5. Определить среднюю кинетическую энергию молекул одноатомного газа и концентрацию молекул при температуре 290 К и давлении 0,8 МПа.
Задача 6. Газ при давлении 8 атм и температуре 120С занимает объем 855 л. Каково будет давление, если эта же масса газа при температуре 470 С займет объем 800 л?
Задача 7. Каково давление сжатого воздуха, находящегося в баллоне вместимостью 20 л при 12 °С, если масса этого воздуха 2 кг?
Решение задач:
1. Средняя квадратичная скорость молекул газа, находящегося при температуре 1000С, равна 540 м/с. Определить массу молекулы.
3. В баллоне емкостью 30 л находится кислород при давлении 72·105 Па и температуре 264 К. Часть газа из баллона выпустили, причем через некоторое время температура газа в баллоне повысилась до 170С, а давление упало до 29·105 Па. Какое количество кислорода выпустили?
4. Газ при давлении 0,2 МПа и температуре 15 °С имеет объем 5 л. Чему равен объем газа этой массы при нормальных условиях?
5. Какой объем займет газ при 77 °С, если при 27 °С его объем был 6 л?
6. При увеличении абсолютной температуры в 1,4 раза объем газа увеличился на 40 см3. Найти первоначальный объем.
7. Температура воздуха в цилиндре 7 °С. На сколько переместится поршень при нагревании воздуха на 20 К, если I = 14 см?
8. Найти абсолютное давление пара в котле, приведенное к 0ºС, если манометр показывает р = 0,2 МПа, а атмосферное давление по ртутному барометру составляет 700 мм рт. ст. при температуре t = 25 ºС.
9. Избыточное давление в паровом котле р = 0,05 МПа при барометрическом давлении В01 = 96900 Па. Чему будет равно избыточное давление в котле, если показание барометра повысится до В02 = 104900 Па, а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 ºС
Домашнее задание
Контрольные вопросы:
1. Какие величины характеризуют состояния макроскопических тел?
2. Каковы отличительные признаки состояний теплового равновесия?
3. Наблюдали ли вы примеры установления теплового равновесия тел, окружающих вас в повседневной жизни?
4. Как зависит интенсивность теплообмена между двумя телами от разности их температур?
5. Чему равен абсолютный нуль температуры по шкале Цельсия?
6. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
7. Каков физический смысл постоянной Больцмана?
8. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул газа?
9. Почему концентрация молекул всех газов одна и та же при одинаковых давлениях и температурах?
10. Температура железного бруска 41оС, а температура деревянного бруска 285 К. Температура которого бруска выше?
11. Как изменится давление идеального газа постоянной массы при увеличении абсолютной температуры и объема в 2 раза?