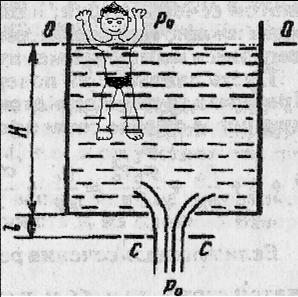
Истечение из донного отверстия в тонкой стенке

Пусть давление на поверхности жидкости в резервуаре равно ро-.
Принимая за плоскость отсчета горизонтальную плоскость, проходящую через сжатое сечение струи (С—С), получим:
Если площадь сечения резервуара много больше площади сечения сжатой струи, то
v0 «
vc и скоростным напором
можно
пренебречь.
Потери напора h1-2 связаны с диссипацией механической энергии за счет сил внутреннего вязкого трения во всем объеме жидкости в резервуаре и местными сопротивлениями в отверстии. Пренебрегая (вследствие их малости) потерями в резервуаре, учтем лишь потери от местного сопротивления на входе в отверстие, представляя их в виде:
,
где vc — скорость в сжатом
сечении.
Если пренебречь также величиною l по сравнению с H, то решая уравнение Бернулли относительно vc, получим (при α= 1)
,
где рС - давление в сжатом сечении.
Введем обозначения
тогда выражение средней скорости в сжатом сечении имеет вид:
ножитель φ называется коэффициентом скорости, он учитывает потери напора при прохождении жидкости через отверстие.
Отношение сжатого сечения wC к сечению отверстия w0, обозначаемое буквой ε, называется коэффициентом сжатия струи.
Очевидно, что в случае круглого отверстия
Размер и форма отверстия влияют на величину ε, вследствие чего ε определяется для данных отверстий и напора опытным путем.
3. Истечение через малые отверстия в тонкой стенке при постоянном напоре
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис 2).
Рис. 2 Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.3, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.3, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны.
Струя, отрываясь от кромки отверстия, несколько сжимается (рис.3, а).
Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.
Рис. 3. Истечение через круглое отверстие
Степень сжатия оценивается коэффициентом сжатия
где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dс и dо - диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
где Н -
напор жидкости, определяется как
φ-
коэффициент скорости
где α - коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е.
μ = εφ.
В итоге получаем расход
где ΔР - расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача - определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям.
На рис.4 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
где ν - кинематическая вязкость.
Рис. 4. Зависимость ε, φ и от числа Reu Рис. 5. Инверсия струй
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5).
Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
4. Истечение при несовершенном сжатии
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.6).
Рис. 6. Схема несовершенного сжатия струи
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров.
При
истечении жидкостей из цилиндрического резервуара круглого сечения через круглое
отверстие, расположенное в центре торцевой стенки, при больших числах Re
коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной
Н.Е. Жуковским:
где n - отношение площади отверстия Sо к площади поперечного сечения резервуара S1
Расход жидкости при несовершенном сжатии
,
где напор Н нужно находить с учетом скоростного напора в резервуаре
5. Истечение под уровень
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.7). такой случай называется истечением под уровень, или истечением через затопленное отверстие.
Рис. 7. Истечение по уровень
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в
сжатом сечении струи
где φ - коэффициент
скорости;
Н - расчетный напор,
Расход жидкости равен
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
ИТОГИ:
Теоретическая скорость истечения (без учета потерь на входе в отверстие)
,
где
- удельная
потенциальная энергия.
Теоретический расход QT = v•S0.
Действительные значения скорости v и
расхода Q
отличаются от теоретических и характеризуются коэффициентами
скорости и
расхода
Действительная скорость v меньше
теоретической из-за потерь на входе в отверстие
, где ζвх -
коэффициент потерь на входе в отверстие.
Действительный расход QT = v•Sструи меньше теоретического не только из-за уменьшения действительной скорости, но и из-за сужения струи.
Выражая Q через теоретическое значение скорости и площадь отверстия, получим:
Q = φ vTε S0 = φε QT = μ QT
т.е. μ = φε .
При истечении через отверстие в боковой стенке закономерности остаются такими же, если d0 = H и отверстие достаточно далеко отстоит от дна.
6. Истечение из насадок. Истечение через насадки при постоянном напоре
Насадком называется присоединенный к отверстию в тонкой стенке короткий патрубок.
Насадки делятся на три основные группы:
цилиндрические — внешние 1 и внутренние II,
конические — сходящиеся III и расходящиеся IV и
коноидальные с закругленными по форме сжатия струи стенками — V.
Истечение через насадок дает нам больший расход, чем через отверстие в тонкой стенке. Но потери будут больше, чем через отверстие. Причина повышения потерь напора кроется в том, что кроме потерь на входе в насадок в связи с острыми краями отверстия возникают еще дополнительные потери при расширении струи от сжатого сечения С-С до поперечного сечения патрубка 1-1.
Записывая, подобно случаю истечения через отверстие с острой кромкой, уравнение
Бернулли, для сечений — одного на поверхности жидкости в сосуде и второго у
выходного отверстия насадка и принимая плоскость сравнения на уровне центра
тяжести выходного сечения насадка, получим (полагая
вследствие
относительной малости этой величины по сравнению с другими членами уравнения)
здесь ро — давление над жидкостью в сосуде;
р — давление во внешней среде, в которую происходит истечение; v — средняя скорость на выходе из насадка;
∑ h — потери напора.
Пренебрегая потерями в сосуде из-за малости, учтем лишь потери в насадке.
Обозначим
и назовем ее напором истечения, тогда получим:
Отметим, что потери напора ∑ h в насадке возникают при обтекании кромок отверстия, при расширении струи и вследствие трения на длине l насадка.
Учитывая все поправки получим:
Выражение перед величиною представляет
собою по смыслу коэффициент скорости при истечении через насадок; сохраняя за
этим коэффициентом обычное обозначение φ, получаем:
Отметим, что для нормальной работы насадка необходимо, чтобы абсолютное давление в сжатом сечении (С-С) было больше, чем давление насыщенных паров жидкости при данной температуре.
7. Режимы истечения жидкости из насадок
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 8). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
1) Первый режим - безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис 8).
Рис. 8. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l/d и числа Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка
P2 - P1 = 0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.9).
2) Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
Рис. 9. Второй режим истечения через насадок
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме - большое сопротивление и недостаточно высокий коэффициент расхода, а на втором - очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа.
На рис.10 даны различные типы насадков и указаны значения соответствующих коэффициентов.
Рис. 10. Истечение жидкости через насадки а - расширяющиеся конические; б - сужающиеся конические; в - коноидальные; г - внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
Пример решения задач:
Задача 1. Определить расход воды через отверстие диаметром 1см и цилиндрический насадок диаметром 1 см. Напор воды Н принять 5м вод. ст.
Задача 2. Вода вытекает из бака через конический сходящийся насадок с минимальным пропуском сечения S=2см2 в ведро емкостью V=10л. Коэффициент расхода насадка μ=0,96. Уровень воды в баке поддерживается постоянным от водопроводной сети. Центр сечения насадка расположен на глубине H=1,2м от поверхности воды в баке. Определить время заполнения ведра водой.
Домашнее задание:
Контрольные вопросы:
1. Что называется насадком? Назовите основные типы насадков.
2. Назовите признаки, характеризующие малое отверстие в тонкой стенке
3. Какова причина сжатия струи при истечении?
4. Коэффициенты сжатия, скорости и расхода, их физический смысл. Как связаны между собой эти коэффициенты?
5. Напишите формулы для расчета скорости и расхода при истечении.
6. Как определить действующий напор при истечении?
7. Какое сжатие называется совершенным, несовершенным, полным, неполным? Каково соотношение между коэффициентами сжатия струи для этих случаев?
8. Почему при истечении через внешний цилиндрический насадок коэффициент скорости меньше, а коэффициент расхода больше, чем при истечении через отверстие?
9. Что называется критическим напором для цилиндрического насадка? От чего зависит его величина?
10. Особенности истечения через насадки различных типов.