Основные закономерности движения жидкости. Законы внутреннего трения.
1. Вязкость жидкостей и газов
Вязкостью называется способность движущейся жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Это свойство противоположно текучести и является причиной возникновения в движущейся жидкости сил трения между ее частицами и между жидкостью и твердым телом (например, жидкостью и стенками трубы, русла, корпусом плавающего тела).
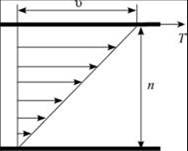
Вязкостью называется способность жидкости оказывать сопротивление сдвигающим усилиям. Это свойство жидкости проявляется лишь при ее движении. Допустим, что некоторое количество жидкости заключено между двумя плоскими неограниченными параллельными пластинами; расстояние между ними – п; скорость движения верхней пластины относительно нижней – υ.
Опыт показывает, что слой жидкости, непосредственно прилегающий к стенке, прилипает к ней. Отсюда следует, что скорость движения жидкости, прилегающей к нижней стенке, равна нулю, а к верхней – υ. Промежуточные слои движутся со скоростью, постепенно возрастающей от 0 до υ.

Таким образом, существует разность скоростей между соседними слоями, и возникает взаимное скольжение слоев, которое приводит к проявлению силы внутреннего трения
Чтобы перемещать одну пластину относительно другой, необходимо приложить к движущейся пластине некоторую силу F, равную силе сопротивления жидкости в результате внутреннего трения.
Ньютон установил, что эта сила пропорциональна скорости v, поверхности соприкосновения S и обратно пропорциональна расстоянию между пластинами n, т.е.
Согласно гипотезе Ньютона закон о трении в движущейся жидкости выражается зависимостью
где: F – сила трения;
S – площадь поверхности соприкосновения между собой слоев движущейся жидкости;
-
производная скорости u по нормали к направлению движения (градиент скорости);
μ - динамический коэффициент вязкости, количественно характеризующий вязкость жидкости.
Для большего уточнения этой зависимости ее следует отнести к бесконечно малому расстоянию между слоями жидкости, тогда
где Δ υ – относительная скорость движения соседних слоев;
Δп – расстояние между ними.
Или в пределе
Последнее выражение представляет закон Ньютона для внутреннего трения.
Знак плюс или минус принимается в зависимости от знака градиента скорости dv/dn.
Так
как есть
касательное напряжение сдвига, то закону Ньютона можно придать более удобный
вид:
Касательное напряжение, возникающее в жидкости, пропорционально градиенту скорости в направлении, перпендикулярном вектору скорости и площадке, по которой оно действует.
Таким образом, сила внутреннего трения в жидкости прямо пропорциональна градиенту скорости dv/dn, площади трущихся слоев S и динамической вязкости μ.
В жидкости сила трения не зависит от давления.
Указанное свойство имеет огромное значение в технике. Вводя жидкость – смазку между трущимися парами, которые в машинах могут соприкасаться, оказывая друг на друга большое давление, заменяют сухое трение трением в жидкости. При этом силы трения уменьшаются, перестают зависеть от давления, значительно снижаются затраты мощности на преодоление сил трения и уменьшается нагрев и износ трущихся поверхностей.
Из приведенного закона вытекает, что
1) Если жидкость находится в покое (v=0), то и градиент скорости
и сила
трения
F
= 0 в покоящейся жидкости силы трения не возникают, свойство
вязкости жидкости не проявляется.
2)
Если при S=1 принять также
то получим μ =
τ , т.е. динамический коэффициент вязкости есть удельная сила трения при
градиенте скорости равном единице.
В
гидравлике для характеристики вязкости жидкости чаще применяется
кинематический коэффициент вязкости n, равный отношению динамического
коэффициента вязкости к плотности жидкости:
Он
имеет размерность
В размерность кинематического коэффициента вязкости не входят единицы силы и массы. Его размерность определяется только кинематическими единицами (длиной и временем). Поэтому коэффициент n называется кинематическим. Он имеет одинаковую размерность во всех системах единиц механических величин.
На практике в качестве единицы измерения кинематического коэффициента вязкости часто применяют стокс:
2. Оценка вязкости жидкости
Процесс определения вязкости называется вискозиметрией, а приборы, которыми она определяется вискозиметрами.
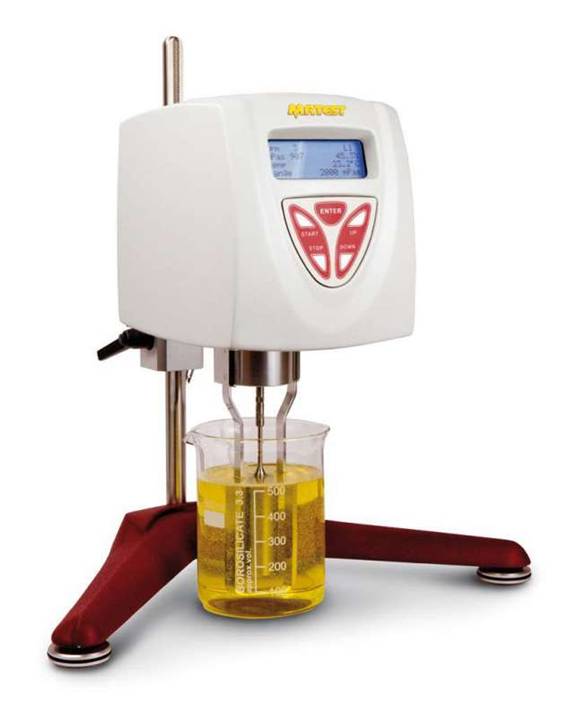
Помимо оценки вязкости с помощью динамического и кинематического коэффициентов пользуются условной вязкостью - градусы Энглера (Е).
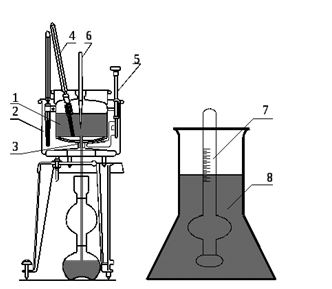
Вязкостью, выраженной в градусах Энглера, называется отношение времени истечения 200 см³ испытуемой жидкости через капилляр d = 2,8 мм к времени истечения такого же объема воды при t = 20 0С
Такой прибор называется вискозиметром Энглера.
Для пересчета градусов Энглера в стоксы для минеральных масел применяется формула
Таким образом, для оценки вязкости жидкости можно использовать три величины, которые связаны межу собой
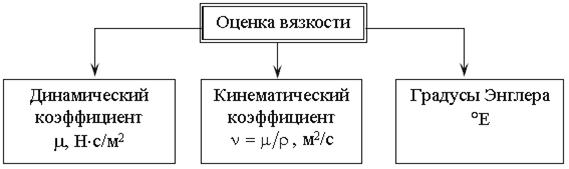
Рис. Способы оценки вязкости жидкости
Итак, для определения вязкости применяются специальные приборы – вискозиметры.
При этом используются закономерности процессов, в которых вязкость играет существенную роль, в частности:
- закон Стокса (сила сопротивления F движению шарика радиуса r, движущегося со скоростью v: F = 6∙p∙m∙r∙v;
- закон Пуазейля (расход жидкости Q при истечении через трубку длиной l, диаметром d при избыточном давлении p-p0:
3. Зависимость вязкости от температуры и давления.
Вязкость жидкостей в большой степени зависит от температуры, при этом вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает. Так, для чистой пресной воды зависимость динамической вязкости от температуры определяется по формуле Пуазейля
Пример решения задач:
Задача Какой наибольшей скорости v может достичь дождевая капля диаметром d = 0,3 мм, если динамическая вязкость воздуха μ=1,2·10-5 Па·с?
Дано:
d = 0,3 мм
η = 1,2·10-5 Па·с
v - ?
где r – радиус капли;
ρ2 – плотность капли (плотность воды);
g – ускорение силы тяжести.
Задачи для самостоятельного решения
Задача 1 Шарик всплывает с постоянной скоростью v в жидкости, плотность ρ1 которой в 4 раза больше плотности ρ2 материала шарика. Во сколько раз сила трения Fтp, действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?
Задача 2. Стальной шарик диаметром d =1мм падает с постоянной скоростью v =0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость μ касторового масла
Домашнее задание:
Контрольные вопросы:
1. Что называется вязкостью жидкости
2. Запишите формулу Ньютона для силы трения
3. Что называется динамической, кинематической вязкостью жидкости
4. С помощью какого прибора определяется вязкость жидкости
5. Запишите формулу Стокса
6. Запишите формулу Пуазейля