Основы гидродинамики.

Гидродинамика, изучая закономерности движения, решает три задачи: внутреннюю, внешнюю и смешанную.

Внутренняя задача связана с анализом движения жидкостей внутри труб и каналов.

Внешняя задача изучает закономерности обтекания жидкостями различных тел (при механическом перемешивании, осаждении твердых частиц в жидкости и т. п.).

Смешанная задача решается при движении жидкости через зернистый слой твердого материала, когда она перемещается как внутри каналов сложной формы, так и одновременно обтекает твердые частицы. Такие условия наблюдаются в процессах фильтрования, массопередачи в аппаратах с насадками, сушки и т. д. Анализ движения жидкостей в случаях такой смешанной задачи гидродинамики проводят приближенно, сводя его к решению внутренней или внешней задачи.

Движущей силой при течении жидкостей является разность давлений, которая создается с помощью насосов или компрессоров, либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить разность давлений, необходимую для перемещения данного количества жидкости с требуемой скоростью, а значит, и расход энергии на это перемещение, или наоборот — определять скорость и расход жидкости при известном перепаде давления.

1. Основные характеристики жидкости в гидравлике

Траекторией называется линия, которую описывает частица жидкости при своем движении.

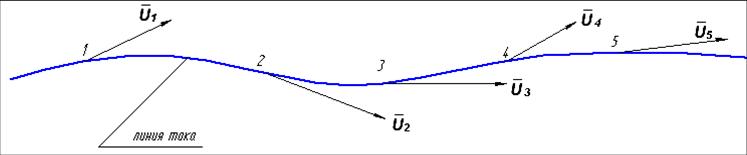
Представим себе, что в точках 1,2,3,4,5 и т.д., находящихся на бесконечно малом расстоянии друг от друга, движущейся жидкости нам известны векторы скоростей v. Линию, проведенную касательно к этим векторам, будем называть линией тока 

Линней тока называется кривая, в каждой точке которой в данный момент времени векторы скорости являются касательными к ней. В случае установившегося движения траектории и линии тока совпадают и неизменны во времени.

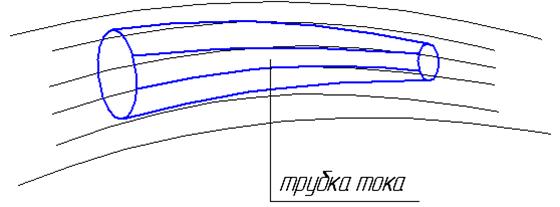
Трубкой тока называется совокупность линий тока проведенных через каждую точку бесконечно малого контура.

Элементарной струqкой называется семейство (пучок) линий тока, проходящих через все точки бесконечно малой площадки dS (или dω), которая перпендикулярна направлению движения.

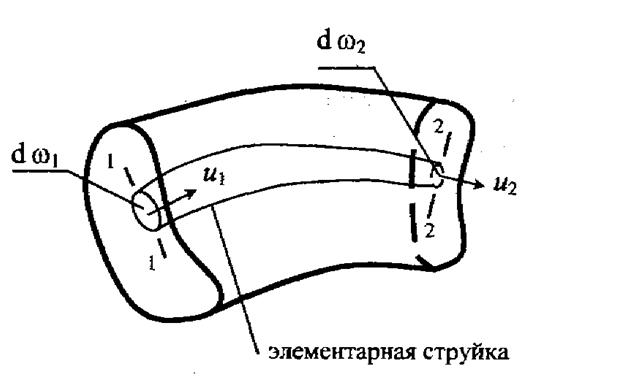
Элементарной струйкой также называется жидкость, движущаяся в трубке тока.

Поток жидкости в соответствии со струйчатой моделью движения жидкости представляет совокупность элементарных струек.

Живым сечением потока называется поверхность, в каждой точке которой вектор скорости направлен по нормали.

Живое сечение потока жидкости характеризуется гидравлическими элементами.

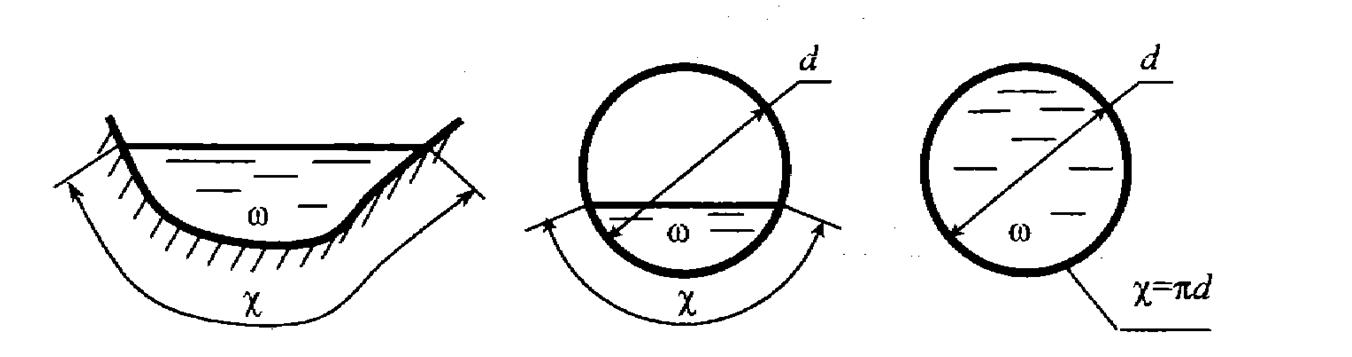
Площадь живого сечения  S (или ω). При решении инженерных задач потоки, как правило, бывают слабо искривленными и живое сечение в этих случаях приближенно можно принять плоским.

Смоченный периметр χ. Это длина линии, по которой жидкость в живом сечении соприкасается с твердыми поверхностями, ограничивающими поток.

Гидравлический радиус R. Это отношение площади живого сечения к смоченному периметру  .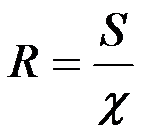  

Так, например, для живого сечения круглой формы радиусом r гидравлический радиус R = r/2.

Расход потока жидкости (расход жидкости) Q– количество жидкости, протекающей через живое сечение потока в единицу времени.

Расход жидкости измеряется обычно в м³/с, дм³/с или л/с.

 Он вычисляется по формуле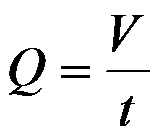

где Q - расход жидкости,

V - объём жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным.

Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

Q = υ_ср * F,

где Q – расход;

υ_ср – средняя скорость потока

F – площадь сечения потока.

Средняя скорость потока жидкости v называется такая одинаковая для всех точек живого сечения скорость движения жидкости, при которой через это живое сечение проходит тот же расход Q, что и при действительных скоростях движения жидкости и.

Количество жидкости, протекающее через живое сечение струйки в единицу времени, называется элементарным расходом. Он бывает объемный, массовый и весовой:

объемный расход dQ = v dw, м³/с;

массовый расход dМ = ρ dw, кг/с;

весовой расход dG = γ v dw, Н/с.

Для потока живое сечение будем считать условно плоским и проведенным нормально к его оси.

Так как по живому сечению потока скорости струек распределяются неравномерно, то для определения объемного расхода необходимо знать закон распределения этих скоростей, что является довольно сложной задачей. Для упрощения определения расхода потока введено понятие средней скорости потока V. Это такая воображаемая скорость, с которой должны двигаться все частицы потока, чтобы расход оказался равным расходу при движении жидкости с действительными неодинаковыми для отдельных частиц скоростями.

Единственный способ определения средней скорости: является

объемный расход    

массовый расход М = ρ vw;

весовой расход G = γ vw.

2. Виды движения жидкости в гидравлике.

Гидродинамика – раздел гидравлики, который изучает законы движения жидкости.

Потоком жидкости называется движущаяся масса жидкости, ограниченная твердыми направляющими поверхностями, поверхностями раздела жидкостей и свободной поверхностью.

Потоки жидкостей и газов классифицируют по различным признакам:

1) Все возможные виды движения жидкости подразделяют на две категории:

- безвихревое (потенциальное) движение, когда вращение элементарных частиц жидкости отсутствует;

- вихревое движение, когда присутствует вращение элементарных частиц жидкости и им пренебречь нельзя.

Среди вихревых движений имеет место частный случай — винтовое движе­ние, при котором вектор угловой скорости совпадает с направлением вектора линейной скорости в данной точке. Движение жидкой частицы отличается от движения абсолютно твердой частицы. Твердая частица может двигаться или поступательно (хотя бы и непрямолинейно), или вращательно, или поступательно с вращением, но ее форма при этом сохраняется неизменной.

Жидкая частица, сохраняя свой объем (если жидкость несжимаемая), может в своем движении, кроме того, и деформироваться. В общем случае она осуществляет все три вида движения, потому движение жидкой части­цы можно разложить на поступательное, вращательное и деформационное — теорема Коши — Гельмгольца.

В частном случае, если в пространстве, в котором находится данная час­тица, скорости во всех точках равны между собой и параллельны друг другу, ее движение поступательное.

2) В зависимости движения жидкости от времени потоки подразделяют на:

- неустановившееся (нестационарное) движение, когда скорость v в выбранной точке пространства зависит от координат х, y,z и изменяется с течением времени t

- установившееся (стационарное) движение, когда скорость v не изменяется с течением времени и зависит только от координат выбранной

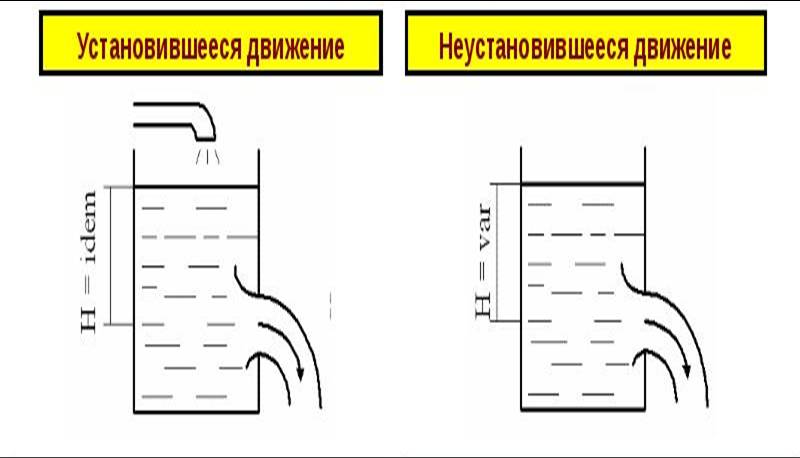
Представим себе движущуюся сплошную среду, каковой является жидкость, например, в лотке переменного в плане сечения. Поместим на поверхности множество миниатюрных корабликов со светящимися лампочками.

Сфотографировав в темноте с определенной выдержкой на пленке, мы получим штрихи, длина которых будет различна, т.е. светящиеся точки движутся с различными скоростями в различных направлениях.

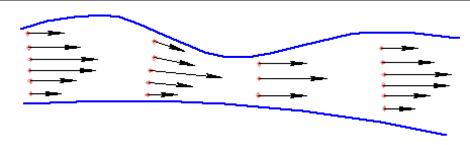
Мгновенная картина скоростей частиц жидкости в пространстве, заполненном жидкостью, называется полем скоростей.

Если бы нам удалось определить в точках движущейся жидкости давление, то мгновенная картина давлений называлась бы полем давлений.

Движущаяся жидкость может иметь два принципиально различных поля: скоростей и давлений.

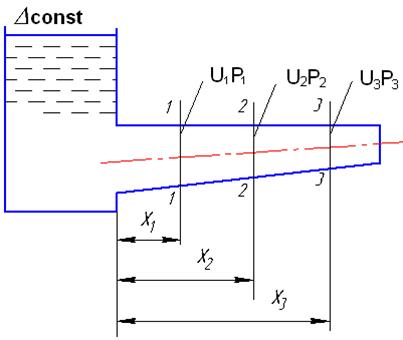
Если поле скоростей и давлений не зависит от времени, то движение называется установившимся, или стационарным. Примером такого движения может быть течение жидкости из резервуара с постоянным уровнем по трубопроводу постоянного или переменного диаметра

Мгновенная картина скоростей частиц жидкости в пространстве, заполненном жидкостью, называется полем скоростей.

Если бы нам удалось определить в точках движущейся жидкости давление, то мгновенная картина давлений называлась бы полем давлений.

Движущаяся жидкость может иметь два принципиально различных поля: скоростей и давлений.

Если поле скоростей и давлений не зависит от времени, то движение называется установившимся, или стационарным. Примером такого движения может быть течение жидкости из резервуара с постоянным уровнем по трубопроводу постоянного или переменного диаметра.

В сечениях 1-1, 2-2, 3-3 и т.д. скорости и давления будут разными, но во времени они останутся постоянными, т.е. поля скоростей и давлений являются функцией только координат  v,р =f(x,y,z).

Если поле скоростей и давлений зависит от времени, то движение называется неустановившимся, или нестационарным.

Примером такого движения может служить опорожнение резервуара по трубопроводу, моменты включения или выключения насосов, закрытие или открытие запорной арматуры и т.п. В этом случае v,р =f(x,у,z,t).

Аналитическое изучение в целом движущейся сплошной среды является сложной задачей. Для понимания физической сущности явлений, происходящих в движущейся жидкости, и возможности их математического описания в классической гидромеханике вводят струйную модель движения жидкости.

3) В зависимости от геометрической формы линий тока и характера изменения поля скоростей потоки делятся:

- с равномерным движением, характеризующимся параллельностью и прямолинейностью линий тока;

- с неравномерным движением. Оно характеризуется тем, что линии тока не являются параллельными прямыми.

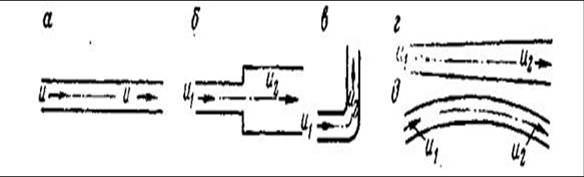
а- равномерное;            б,в – не равномерного            г,д –плавно изменяющееся

4) Площади живых сечений и средние скорости переменные по длине потока.

а) плавно изменяющееся движение (угол расхождения между линиями тока или их кривизна мала, живые сечения принимаются плоскими);

б) резкоизменяющееся движение (угол расхождения между линиями тока или их кривизна велики, живые сечения криволинейны).

5) В зависимости от характера границ потоки делятся на:

- напорные потоки, которые со всех боковых сторон ограничены твердыми стенками;

- безнапорные потоки, которые частично ограничены твердыми стенками и частично свободной поверхностью;

- гидравлические струи, которые ограничены только жидкостью или газовой средой, а твердых границ не имеют.

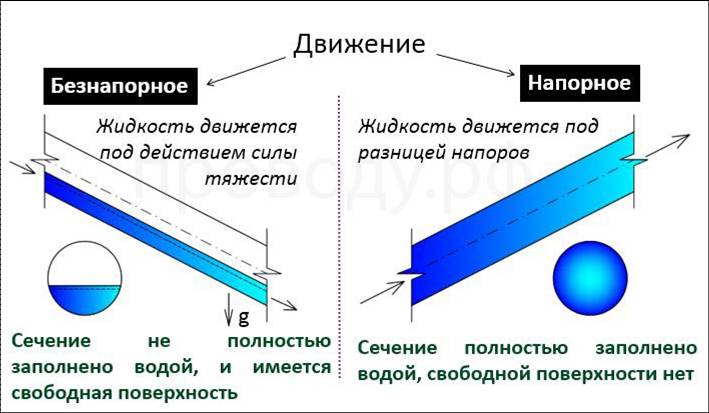
На рисунке  показано течение в трубопроводе, подающем воду из одного резервуар в другой. Если представить, что внутри трубопровода в сечении 1—1 установлен невесомый бесконечно тонкий поршень площадью Sо, то легко понять, что его перемещение будет слева направо под действием разницы сил давлений Р₁ и Р₂, определяемых напорами H₁ и H₂,  

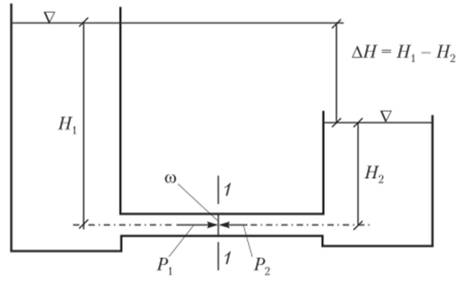
Безнапорное движение – это движение жидкости под действием сил тяжести и при наличии свободной поверхности (каналы, реки, канализационные системы). В этом случае обеспечивается геометрический уклон

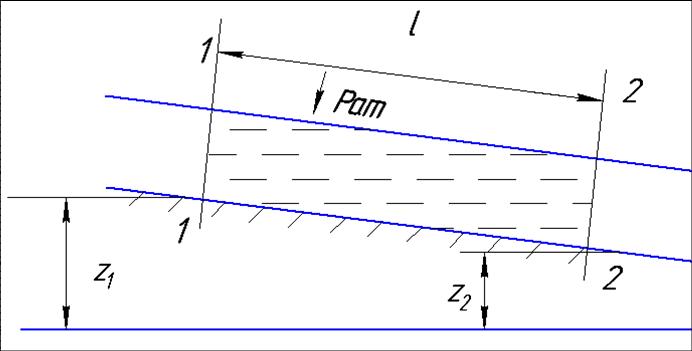
Напорное движение жидкости в потоке – это, как правило, движение без свободной поверхности. Условием такого движения должна быть разность давлений по длине потока: р₁>р₂.

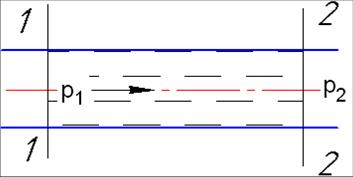
6) Потоки жидкости подразделяются на трехмерные (пространственные), двухмерные (плоские) и одномерные.

При трехмерном течении параметры течения жидкости зависят от трех координат — х, у, z. Обычно такое течение наблюдается в руслах с изменяющимися геометрическим характеристиками или при повороте потока.

Трехмерное движение мо­жет быть как неустановившимся, так и установившимся.

Примером трехмерного движения в прямоугольной системе координат мо­жет служить обтекание потоком любого тела конечных размеров, например, крыла. Если проследить, как изменяется скорость потока вдоль каждой из трех координат, то видно, что при фиксированном значении двух любых ко­ординат (например, у = z = 0) скорость изменяется вдоль третьей координаты. Напомним, что изменение скорости вблизи твердой поверхности обусловлено «прилипанием» частичек жидкости к этой поверхности.

Двухмерным (плоским) течением считается течение с характеристиками, зависящими только от двух координат, например х, y. Такое течение характерно для относительно широких русел.

Оно также может быть неустано­вившимся и установившимся.

Примером двухмерного движения в прямоугольной системе координат может служить обтекание потоком бесконечного цилиндра. Не­трудно заметить, что в отличие от предыдущего случая здесь происходит из­менение скоростей только вдоль осей у и z. Вдоль оси х скорость не изменя­ется при любых фиксированных значениях у и z.

Двухмерное движение всегда является плоскопараллельным, удовлетво­ряющим двум условиям:

а) в данный момент времени область движения можно пересечь такими плоскими параллельными поверхностями, в которых лежат векторы скоро­стей и ускорений, отвечающие всем точкам этих поверхностей;

б) во всех точках любого перпендикуляра, проведенного к указанным по­верхностям, скорости и ускорения в данный момент времени одинаковы (по величине и направлению).

Одномерное движение — это такое движение, когда параметры потока изменяются только вдоль одной координаты.

Примером одномерного движения в прямоугольной системе координат мо­жет служить обтекание потоком бесконечной плоской пластины (рис.3). В этом случае скорость изменяется только в направлении нормали к поверхнос­ти пластинки, т. е. вдоль координаты у. Одномерное течение также всегда явля­ется плоскопараллельным. Его называют также линейным движением.

Вполне очевидно, что одномерное движение является простейшим для анализа видом движения. При этом следует отметить, что иногда от выбора системы координат зависит, будет ли движение трехмерным, двухмерным или даже одномерным. Например, при движении жидкости в цилиндричес­кой трубе переход от прямоугольной к цилиндрической системе координат переводит задачу из двухмерной в одномерную.

Одномерным называют течение, в котором основные параметры зависят лишь от одной координаты, например х направление которой совпадает с направлением вектор средней скорости. Такими можно считать большинство течений, рассматриваемых в технической гидравлике, для ни[ основными параметрами с прикладной точки зрения являются расход потока, средняя скорость течения, закон изменения давления или глубины но длине русла. При решении большинства инженерных задач применения одномерно модели течения бывает вполне достаточно.

7. Движение может быть сплошным и прерывистым. 

Сплошным, или не­прерывным движением, называется такое движение, при котором жидкость сплошь заполняет всю область своего движения. 

Прерывистым является движение жидкости при наличии пустот в области движения. Обычное тече­ние в реках — сплошное, а на водопадах — прерывистое.

8. Движение может быть осесимметричным (поле скоростей и ускорений име­ет одинаковый вид в любых плоскостях, проходящих через некоторую прямую, называемую осью симметрии) и неосесимметричным. Примером осесимметричного движения может служить движение жидкости в круглых трубках.

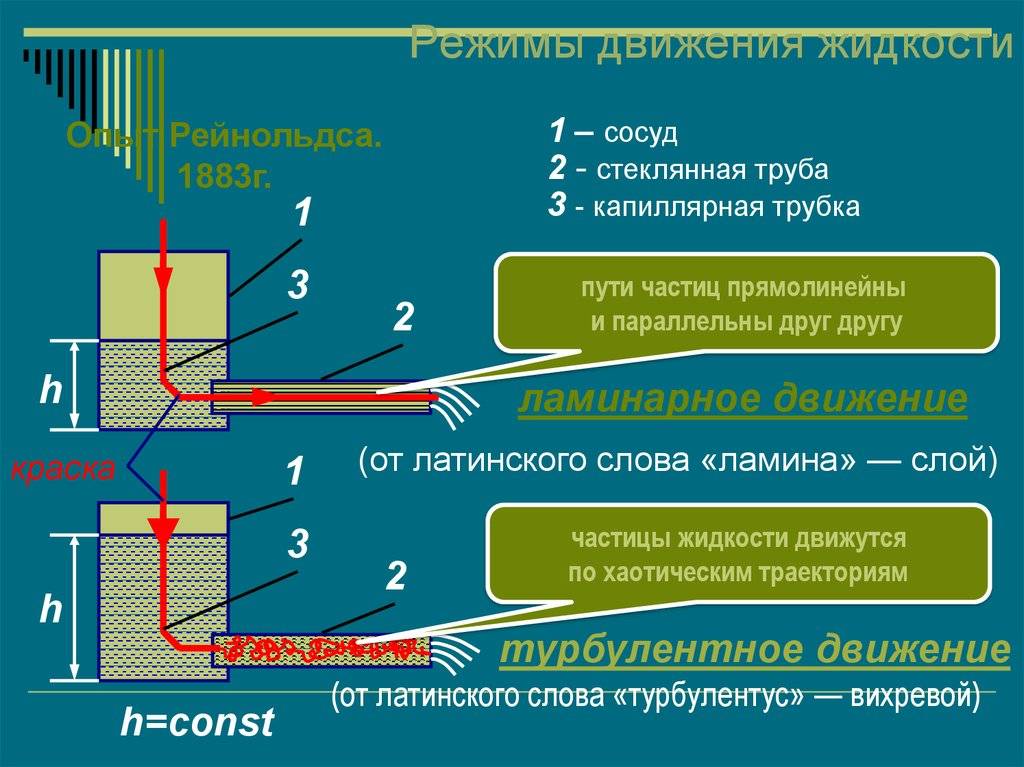
9. Движения можно классифицировать по механизму передачи количест­ва движения между слоями жидкости. Если этот механизм имеет молекуляр­ную природу, движение называется ламинарным. Если количество движения передается в основном за счет обмена жидкими массами, перемещающимися хаотически во всем объеме жидкости, движение называется турбулентным. Турбулентное движение можно дополнительно разделить на движение в зо­нах гладкого, смешанного и шероховатого сопротивления (трения).

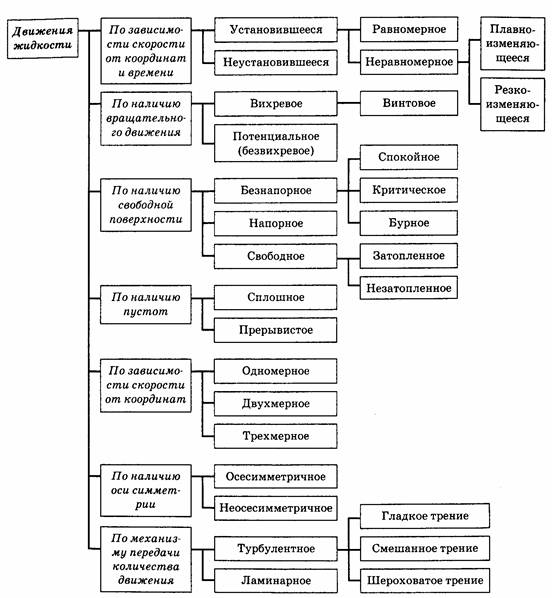
Для лучшего представления о связи между различными видами движе­ния на рис.4. показана классификационная схема движений по Л. С. Абразону, пользуясь которой, можно достаточно полно охарактеризовать любое течение

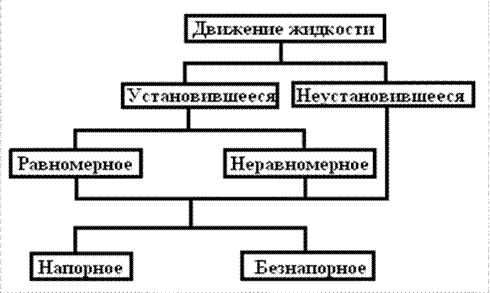
Наряду с приведенными существуют и другие классификации потоков жидкости.

Примеры решения задач:

Задача 1. Найти скорость v течения углекислого газа по трубе, если известно, что за время t = 30 мин через поперечное сечение трубы протекает масса газа m= 0,51 кг. Плотность газа ρ=7,5 кг/м³.

Задача 2. Определить скорость движения жидкости в подводящей линии и скорость поршня, если диаметр трубопровода 0,012м, диаметр поршня 0,07м, подача насоса Q=1,7·10^-3м³/с

Задача 3 Струя воды ударяется о вертикальную стенку, расположенную перпендикулярно струе. После удара вода стекает вниз по стене. Найти силу, с которой струя действует на стену, если площадь струи 5см², а ее скоростью v=8 м/с.

Домашнее задание:

Контрольные вопросы:

1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется

(живым сечением).

2. Часть периметра живого сечения, ограниченная твердыми стенками называется (смоченный периметр)
3. Объем жидкости, протекающий за единицу времени через живое сечение называется (расход потока)

4. Отношение расхода жидкости к площади живого сечения называется (средняя скорость потока)
5. Отношение живого сечения к смоченному периметру называется (гидравлический радиус потока)

6. Какой буквой обозначается расход?(Q)

7. Какой буквой обозначается  живоt сечения? (w)

8. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется (линия тока).

9. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется (трубка тока)

10. Что называется элементарной струйкой (часть потока, заключенная внутри трубки тока)

11 Течение жидкости со свободной поверхностью называется (безнапорное);
12. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется (напорное);
13. Запишите уравнения установившегося движения жидкости

14. Запишите уравнения неустановившегося движения жидкости

15. На какие виды делятся движения по наличию вращательного движения частиц жидкости

16. Назовите вид движения, при котором параметры потока изменяются только вдоль одной координаты.

17. Для какого движения характерно наличие пустот в области движения