Законы гидростатики Основные законы равновесия состояния жидкости

Гидростатика – раздел гидравлики, изучающий законы равновесия жидкости и их применение.

1. Гидростатическое давление

Напряжение в жидкости описывается давлением.

Давление (р) – величина, равная отношению модуля силы давления F, действующей перпендикулярно поверхности, к площади этой поверхности.

(Н/м²)

При равномерном распределении сил давления, давление на всех участках поверхности одинаково и численно равно силе давления, действующую на поверхность единичной площади.

В гидростатике изучают жидкость, находящуюся в покое. Касательные напряжения в ней равны нулю. Считается также, что жидкость неспособна сопротивляться растягивающим усилиям. Поэтому будем считать, что в любой точке жидкости имеется только нормальное напряжение σ = σ_н.

Гидростатическим давлением в данной точке называют скалярную величину, равную значению напряжения в рассматриваемой точке: ρ = |σ|, где |σ| - значение напряжения.

Если на жидкость действует какая-то внешняя сила, то говорят, что жидкость находится под давлением. В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находя

Рассмотрим наиболее важный для практики частный случай равновесия жидкости, находящейся под действием только сил тяжести.

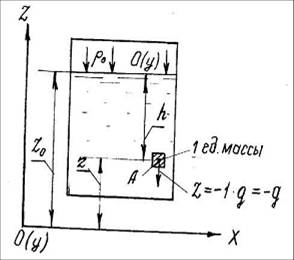
Рассмотрим закрытый сосуд, в котором находится жидкость.

Обозначим через р₀ внешнее поверхностное давление, т.е. давление на свободную поверхность жидкости.

Наметим точку А, у которой выделим единицу массы жидкости. К этой единице массы приложена объемная сила – сила тяжести.

Рассмотрим абсолютный покой несжимаемой жидкости в поле силы тяжести. .

f_x =0

f_y =0

f_z = -g

Тогда уравнение Эйлера примет вид: dp=-ρgdz.

 Проинтегрировав и поделив уравнение на удельный вес

для двух точек одного и того же объёма жидкости можно записать

- основной закон гидростатики

Последняя формула - гидростатический закон распределения давления, состоящий в том, что в тяжелой (подверженной действию силы тяжести) несжимаемой жидкости давление линейно зависит от вертикальной координаты.

Чтобы найти постоянную в уравнении надо использовать какое-нибудь граничное условие.

Пусть, например, жидкость покоится в резервуаре.

Тогда давление в произвольной точке А выразится зависимостью:

Р = - ρ gZ + (р₀+ρ gZ₀) или р = р₀ +ρ g(Z₀-Z) = р₀+ρ gh.

Давление р, определяемое по этой формуле, называется абсолютным давлением.

р_абс = р₀+ ρgh- уравнение и является основным уравнением гидростатики в простейшей гидравлической форме.

Величина ρgh представляет собой ту часть абсолютного давления р_абс, которая обусловлена весом самой жидкости. Назовем ее весовым давлением.

р_вес=ρ gh.

2. Виды давлений

Различают следующие виды давления: барометрическое, абсолютное, избыточное, вакуум.

Барометрическое (атмосферное) давление зависит от высоты места над уровнем моря и от состояния погоды. За нормальное барометрическое давление принимают 760 мм.рт.ст. На свободную поверхность водных потоков, а также естественных и искусственных водоемов действует барометрическое давление.

1) Абсолютным (полным) давлением р называется давление, определяемое по формуле

Основное уравнение гидростатики показывает, что абсолютное давление в точке равно сумме внешнего поверхностного давления р₀ и весового давления(ρgh)

р_абс = р₀+ ρgh,

где р₀ - давление на свободной поверхности. Если на свободной поверхности давление равно атмосферному, то разность

2) Разность между абсолютным гидростатическим давлением и атмосферным называется избыточным или манометрическим давлением (такое давление показывает механический манометр):

р_изб = р_абс – р_ат.

 Из последней зависимости следует, что избыточное давление изменяется с глубиной по линейному закону; оно иногда называется манометрическим.

3) Если давление в точках какого-либо объема жидкости или в закрытых сосудах на свободной поверхности меньше атмосферного (p< p_ат ), то говорят, что в рассматриваемом пространстве вакуум.

Вакуумом называется разность между атмосферным давлением и давлением в разреженном пространстве; иначе говоря, вакуум есть недостаток величины данного давления до атмосферного.

Обозначая величину вакуума через p_в , а давление в разреженном пространстве через p_разр , получим

p_в = p_ат - p_раз 

4) Если р₀ = р_атм, то из основного уравнения гидростатики следует, что

р_абс = р_атм+ρ gh и р_абс – р_атм= р_изб = ρ gh

т.е. избыточное давление равно весовому.

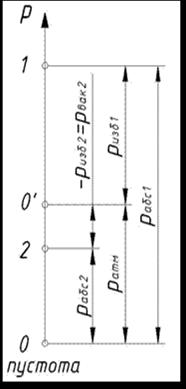
Рисунок. Система отсчета давления

По основному уравнению гидростатики можно определить абсолютное давление в любой точке покоящейся жидкости.

Если взять ряд точек, в которых гидростатическое давление одинаково, и провести через эти точки поверхность, то получим поверхность равного давления.

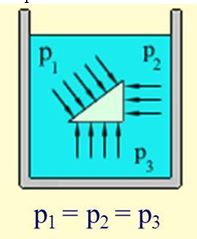
3. Закон Паскаля

Давление, оказываемое на жидкость, передается жидкостью одинаково во всех направлениях.

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массивная сила-сила тяжести и получим уравнение, позволяющие находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это основное уравнение гидростатики:

р_абс = р₀+ ρgh

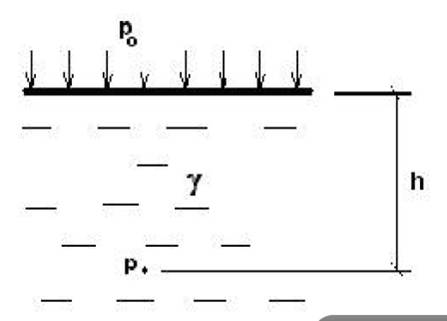
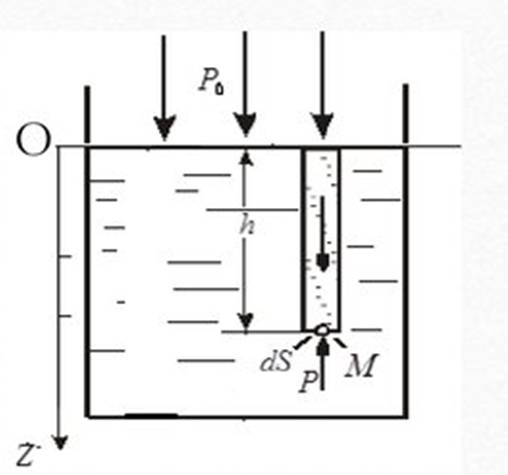
Следствие: Закон Паскаля: Давление свободной поверхности жидкости р₀ одинаково передается всем точкам жидкости по всем направлениям

р_абс - р₀ = ρgh = hγ

 4. Закон Архимеда

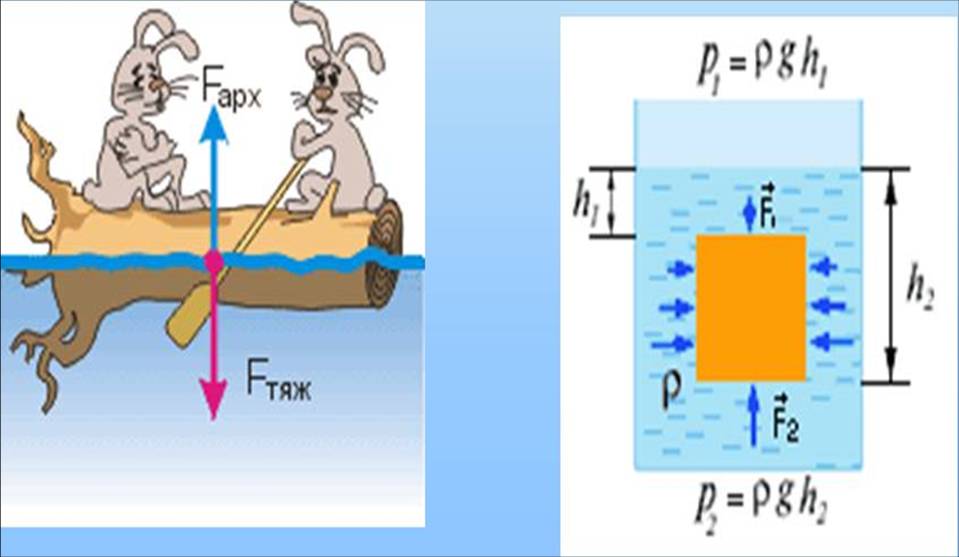
На тело, погруженное в жидкость, действует выталкивающая сила (сила Архимеда). Выталкивающая сила равна по модулю (и противоположна по направлению) силе тяжести, девствовавшей на вытесненным телом объем жидкости, и приложена к центру тяжести этого объема.

F_а = ρ_жgV_т - Закон Архимеда

Причина возникновения выталкивающей силы в разности давлений на разных глубинах (высотах).

Примеры решения задач

Задача 1. B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает? 

 Задача 2. Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?

Задача 3. Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.

h = 5 м

Р₀ = 100 кПа

Р-?

Решение: Вспоминаем основное уравнение гидростатики и записываем:

Р = Р₀ + ρ g h = 100 ·10³ + 10³·10·5 = 150· 10³ ПА

Ответ: 150 кПа.

Задача 4. Давление в паровом котле Р = 0,4 бар при барометрическом давлении 725 мм рт. ст. Чему будет равно избыточное давление в котле, если показание барометра повысится до 785 мм рт. ст., а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 °С.

Дано:

Р_изб1 = 0,4 бар

Р_атм1 = 725 мм рт. ст.

Р_атм2 = 785 мм рт. Ст

Р_изб2 -?

Решение: р_изб = р_абс – р_ат.

р_абс = р_{изб +} р_ат.

Абсолютное давление в котле Р_абс1 = 400000 + 725 ·133,3 = 136642 Па.

Избыточное давление при показании барометра 785 мм рт. ст.

Р_изб2 = 136642 – 785· 133,3 = 32000Па.

Задача 5. Сколько деревянных бревен каждое длиной l=3 м и диаметром d=0,3 м нужно связать, чтобы сделать плот, удерживающий на плаву груз массой m=2000 кг, плотность дерева ρ =500 кг/м³, плотность воды ρ _в=1000 кг/м³?

Дано:

l =3 м

d = 0,3 м

m = 2000 кг,

ρ_д =500 кг/м³,

ρ_в = 1000 кг/м³?

N-?

Задача 6. В цилиндрическую мензурку налиты ртуть и вода в равных по массе количествах. Общая высота двух слоев жидкости равна 29,2 см. Найдите высоту каждой жидкости и давление на дно мензурки. Плотность ртути ρ = 1,36 • 10⁴ кг/м³, воды ρ_в = 1 • 10 ³ кг/м³. Атмосферное давление не учитывается

Дано:

H=29,2 см                                

ρ₁ = 1,36 • 10⁴ кг/м³                     

ρ₂ = 1 • 10 ³ кг/м³

p₁-?

р₂-?

Решение: Пусть h₁ - высота столба ртути, а h₂ - высота столба воды.

По условию задачи h₁+ h₂=H.

Масса ртути в цилиндре m₁=ρ₁V₁=ρ₁Shm₁, где S - площадь основания цилиндра.

Масса воды m₂=ρ₂Sh₂.

Получаем систему уравнений:

h₁ + h₂=H,

Задачи для самостоятельного решения

1. Полый медный шар диаметром d=5 см плавает в воде в состоянии безразличного равновесия. Найти толщину стенок шара. Плотность воды ρ _в=1000 кг/м³, плотность меди ρ_м =8900кг

2. Определить избыточное давление на глубине 4 м. Примем плотность воды ρ =1000 кг/м³ .

3. Жидкостью какой плотности заполнен бак, имеющий форму куба со стороной 10 см, если сила давления на дно равна F=7 Н? Атмосферное давление не учитывается

4. Определите высоту водонапорной башни, если манометр, установленный у ее основания, показывает давление 120 кПа. 

5. Какова плотность жидкости, если на глубине 20 см давление этой жидкости равно 3,6 кПа. Атмосферное давление не учитывается

6. Определите высоту водонапорной башни, если давление в трубах у ее основания равно по показаниям манометра 320 кПа.

Домашнее задание:

Контрольные вопросы

1. Как вы понимаете свойство жидкости – текучесть?

2. От чего зависит вязкость жидкости?

3. Жидкость находится под давлением. Что это означает?

4. Чем отличается плотность от удельного веса?

5. Какое давление называется вакуумметрическим?

 6. В каких случаях возникает избыточное давление?

7. Какие приборы применяют для измерения атмосферного давления?

8. Почему атмосферное давление измеряется в миллиметрах ртутного столба?

9. В чем состоит физический смысл основного уравнения гидростатики?

10. В каких единицах измеряется давление в системе измерения СИ?

11. Если давление отсчитывают от абсолютного нуля, то его называют (абсолютным)

12. Если давление отсчитывают от относительного нуля, то его называют: (избыточным)

13. Если давление ниже относительного нуля, то его называют (давление воздуха)

14. Какое давление обычно показывает манометр? (избыточное)

15. Чему равно атмосферное давление при нормальных условиях?

16. Что определяет давление?