Различные случаи теплообмена излучением

1. Основные понятия.

Энергия излучения переносится электромагнитными колебаниями и фотонами. Генерация лучистой энергии происходит в результате сложных внутриатомных и молекулярных процессов. Всякое тело, имеющее температуру, отличную от абсолютного нуля, способно излучать лучистую энергию.

Наряду с потоком лучистой энер­гии от более нагретых тел к менее нагретым всегда имеется и обрат­ный поток энергии от менее нагретых тел к более нагретым. Конеч­ный результат такого обмена и представляет собой количество переданной излучением теплоты.

Лучистый теплообмен связан с двойным превращением энергии:

- на поверхности тела-излучателя теплота трансформируется в энергию электромагнитных колебаний, которая распространяется в лучепрозрачной среде (или в вакууме) и

- при поглощении ее каким-либо другим телом вновь превращается в теплоту.

Существуют различные виды электромагнитного излучения:

- γ - излучение,

- рентгеновское излучение,

- радиоволны и др.

Однако способностью трансформироваться в теплоту обладает излучение све­тового диапазона (длина волн λ= 0,4-0,8 мкм) и в наибольшей мере инфракрасного диапазона (λ  = 0,8-400).

Излучение всех тел зависит от температуры. С увеличением температуры излучение увеличивается, так как увеличивается внутренняя энергия тела. Зависимость интенсивности передачи теплоты от температуры при излучении значительно большая, чем при теплопроводности и конвекции. Поэтому при низких температурах главную роль играет конвективный теплообмен, а при высоких – теплообмен излучением.

Отношение количества энергии, излучаемой поверхностью тела во всем интервале длин волн спектра ко времени, называют пол­ным (интегральным) лучистым потоком Q (Вт).

Излучение, соответствующее какой-либо определенной длине волны (точнее, узкому интервалу длин волн), называется монохроматическим.

Величина, численно равная количеству энергии, излучаемой единичной поверхностью тела в единицу времени, называется излучательной способностью тела Е (Вт/м²), или плотностью интегрального излучения.

Распределение энергии излучения по длинам волн характеризуется интенсив­ностью излучения E_l, которая представляет собой излучательную способность тела в интервале длин волн от λ до λ + dλ, отнесенную к рассматриваемому интервалу длин волн dλ

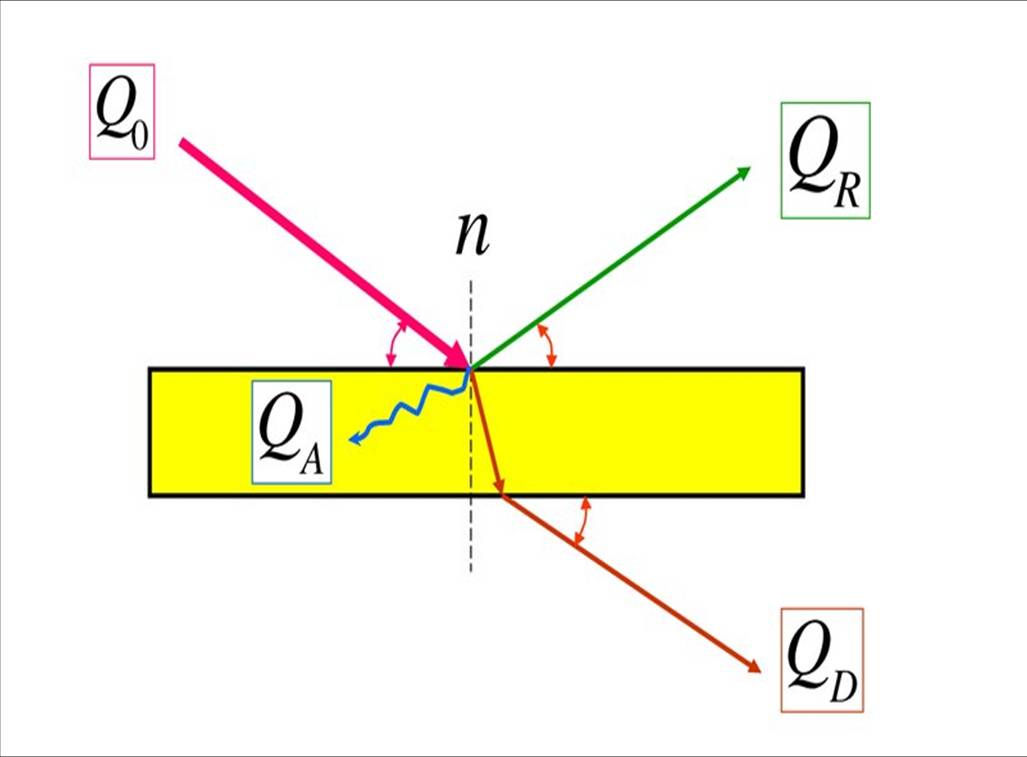
Пусть Q количество лучистой энергии, падающей на тело. В общем случае часть энергии Q_A поглотится телом, часть Q_R , отразится, а часть, Q_D, пройдет сквозь тело

Уравнение баланса энергии имеет вид

Q = Q_A + Q_R + Q_D.

Разделив обе части равенства на Q и обозначив 

А = Q_A/Q, - коэффициент поглощения

R = Q_R/Q, - коэффициент отражения

D = Q_D/Q, коэффициент пропускания

получим   A + R + D = 1.

В предельных случаях A = 1 (R = D = 0) – абсолютно черное тело; 

R = 1 (A = D = 0) – абсолютно белое тело; 

D = 1 (A = R = 0) – абсолютно прозрачное тело.

В природе абсолютно черных, белых и прозрачных тел не существует, тем не менее, понятие о них является важным для сравнения излучательной способности реальных тел.

Оконное стекло прозрачно для световых лучей, а для ультрафиолетовых и тепловых почти непрозрачно. Белая поверхность (ткань, краска) хорошо отражает лишь видимые лучи, а тепловые лучи поглощает также хорошо, как и темная. Свойство тел поглощать или отражать тепловые лучи зависит в основном от состояния поверхности, а не от ее цвета.

2. Основные законы теплового излучения.

2.1 Закон Планка. Устанавливает зависимость интенсивности излучения абсолютно черного тела от температуры Т и длины волны λ:

где C₁ = 3,74·10^-16 Вт/м²; 

C₂ = 1,44·10^-2 м·К.

Графическое представление закона Планка  показано на рисунке.

Из приведенных на графике изотерм видно, что интенсивность излучения вначале, в области коротких волн, быстро возрастает до максимума, а затем медленно убывает, не достигая нулевого значения даже при наи­больших длинах волн, еще соответствующих тепловому излучению.

На графике заштрихованная площадь, ограниченная изотермой, со­ответствующей длинам волн λ до l + dλ, определяет количество энер­гии, излучаемой с единицы поверхности тела в единицу времени при температуре Т в интервале длин волн d λ. 

Иначе говоря, математическое выражение для заштрихованного элемента площади Е_λ0dλ = dE₀.

Полное количество энергии, которую излучает абсолютно черное тело во всем спектре длин волн, будет равно

и может быть графически изображено в виде площади под соответствующей изотермой.

Реальные тела не поглощают всей падающей на них лучистой энергии, имеют А < 1 и являются нечерными. В свою очередь все нечерные тела могут быть разделены по характеру спектра поглощения (излучения) на серые тела и тела с селективным излучением.

Серым называется тело, имеющее сплошной спектр излучения, подобный спектру излучения черного тела, но при меньших значениях интенсивности излучения.

Отношение энергии Е, излучаемой серым телом, имеющим тем­пературу Т, к энергии излучения абсолютно черного тела Е₀ при той же температуре называется степенью черноты e:

К серым телам может быть отнесено большинство твердых тел и капельных жидкостей.

Тела с селективным излучением могут излу­чать и поглощать энергию лишь в определенных, характерных для каждого тела, областях спектра, имеют полосовой спектр излучения. Селективными свойствами обладают многие газы и пары.

2.2 Закон Вина. Длину волны, которой соответствует максимум теп­лового излучения, можно определить из условия Е_λ0 /dλ = 0.

При этом получается:

λ_maxТ = 2,9×10^-3 м×К.

Это уравнение выражает закон смещения Вина, формули­руемый следующим образом: с повышением температуры мак­симум излучения смещается в сторону более коротких волн. Приближенно закон Вина используют и применительно к серым телам.

2.3 Закон Стефана-Больцмана. Он определя­ет зависимость излучательной способности абсолютно черного тела от температуры. Согласно закону Стефана-Больцмана величина Е₀прямо пропорциональна абсолютной температуре в четвертой степени:

Е₀ = σ₀Т⁴,

где σ₀ – константа излучения абсолютно черного тела, численно равная 5,67×10^-8 Вт/(м²×К⁴).

Для практических расчетов это уравнение используют в другой, более удобной форме, имеющей вид

Е₀ = С₀ (Т/100)⁴,

где С₀ = 5,67 Вт/(м²·К⁴) коэффициент излучения абсолютно черного тела.

Для серых тел также можно пользоваться приведенной формулой, но с другим (меньшим) коэффициентом излучения С, т. е.

Е = С (Т/100)⁴ = e·С₀(Т/100)⁴,

где e – степень черноты.

Степень черноты показывает, насколько данное тело приближается по своим излучательным свойствам к абсолютно черному; она зависит от состояния поверхности тела (прежде всего шероховатости) и ее температуры. Значения e для различных тел приводятся в справочной литературе.

2.4 Закон Ламберта. С помощью закона Стефана-Больцмана можно определить общее количество энергии, излучаемой телом по всем направлениям. Однако распределение этой энергии по различным направлениям оказывается неодинаковым. Согласно закону Лам­берта количество энергии Е_j излучаемой телом в направлении, сос­тавляющем с нормалью к поверхности угол j, определяется по урав­нению

Е_j = Е_пcos(j),

где Е_п – количество энергии, излучаемой в направлении нормали к поверхности тела (j = 0).

Интегрирование этого уравнения дает соотношение Е = p×Е_п, т. е. полная лучеиспускательная способность тела в p раз больше лучеиспускательной спо­собности тела в направлении нормали. Опыт показывает, что закон Ламберта строго справед­лив только для абсолютно черного тела. У серых тел этот закон подтверж­дается лишь в пределах j = 0-60°.

2.6 Закон Кирхгофа. 

Закон устанавливает связь между излучательной и поглощательной способностью тела. Закон может быть сформулирован так: отношение лучеиспускательной способности к поглощательной для всех тел одинаково и равно лучеиспускательной способности абсо­лютно черного тела при той же температуре.

Математическое выраже­ние закона Кирхгофа:

Из закона следует, что а так как ,

можно сформулировать закон Кирхгофа иначе: поглощательная способность и степень черноты тела численно равны между собой.

Из закона Кирхгофа следует, что лучеиспускательная способность тел тем больше, чем больше их поглощательная способность. Тела, которые хорошо отражают лучистую энергию, сами излучают очень мало. Поэтому в тех случаях, когда хотят уменьшить потери теплоты каким либо аппаратом, его поверхность обрабатывают так, чтобы она имела наименьшее значение e.

2.7 Законы лучеиспускания газов.

Газы излучают и поглощают энергию излучения. Они не способны ее отражать и рассеивать. Одно – и двухатомные газы (гелий, инертные газы, водород, азот, кислород и др.) практически прозрачны для излучения и не излучают тепловую энергию (до 3000К). Трехатомные газы, например СО₂ и Н₂О, обладают заметным излучением.

Излучение газов носит объёмный характер, так как в нем участвуют все частицы газа. Газы имеют линейчатый спектр излучения. Поглощение и излучение электромагнитных волн происходит только в определенных интервалах длин волн. В остальной части спектра они прозрачны. Полное излучение газа слагается из излучения всех его полос.

С увеличением температуры начинаются процессы ионизации и рекомбинации атомов и молекул. В результате интенсивность излучения увеличивается и отдельные полосы излучения начинают сливаться в сплошные участки.

Законы лучеиспускания газов значительно отлича­ются от законов лучеиспускания твердых тел. Одно- и двухатомные газы практически являются прозрачными телами; их излучательная и поглощательная способность ничтожна.

Спектр излучения и пог­лощения многоатомных газов (NH₃, СО₂, Н₂О и др.) имеет селективный характер; эти газы излучают и поглощают энергию лишь в определенных интервалах длин волн.

В отличие от твердых тел из­лучение и поглощение энергии газами происходит не в поверхностном слое, а во всем объеме. При этом по мере прохождения тепловых лучей через многоатомные газы их энергия уменьшается. Это ослабление зависит от рода газов, температуры и числа находящихся на пути луча молекул. Число молекул пропорционально толщине слоя газа l и плотности газа (т. е. парциальному давлению р_i).

Излучение газов не подчиняется закону Стефана-Больцмана. Однако для технических расчетов условно принимают, что интегральное излучение газов, как и излучение твердых тел, пропорционально четвертой степени их абсолютной температуры:

Е_г = e_г·σ₀(Т)⁴,

где e_г – степень черноты газов, e_г = f(p_i, λ, T).

3. Теплообмен излучением между телами.

Теплообмен излучением между плоскопараллельными поверхностями.

Рассмотрим две бесконечно большие плоскопараллельные поверхности из разнородных материалов разделенные прозрачной средой. Для одной поверхности степень черноты e₁ и температура Т₁, а для другой e₂ и Т₂. Пусть Т₁ > Т₂.

Тогда собственное излучение:

для первой пластины 

для второй пластины 

Результирующая излучательная способность первой пластины на вторую

где e_п – приведенная степень черноты

4. Теплообмен излучением между телом и оболочкой.

Рассмотрим случай, когда теплообмен происходит между телом произвольной формы (не вогнутым) и поверхностью другого, большего тела. При этом поверхность большего тела полностью охватывает меньшее. Для первого тела степень черноты e₁, температура Т­₁ и площадь поверхности F₁, а для второго e₂, F₂ и Т₂. Пусть Т₁ > Т₂.

В этом случае результирующая излучательная способность первого тела на второе

,

где

Если F₂ >> F₁, то e_п >> e₁. Следовательно, если необходимо рассчитать потери теплоты телом в окружающую среду, то можно принять F₂ = ∞, а e_п = e₁, тогда расчетное выражение примет вид 

5. Теплообмен излучением между произвольно расположенными телами.

Рассмотрим случай, когда теплообмен происходит между телами произвольной формы расположенными в пространстве произвольно. Для первого тела степень черноты e₁, температура Т­₁ и площадь поверхности F₁, а для второго e₂, F₂ и Т₂.

Пусть Т₁ > Т₂.

В этом случае только часть энергии излучения будет попадать с одного тела на другое.

Результирующий тепловой поток первого тела на второе можно рассчитать по формуле:

,

где

φ₁₂, φ₂₁ – соответственно угловой коэффициент первого тела относительно второго и второго тела относительно первого.

Угловой коэффициент характеризует долю энергии, которая попадает с тела, площадью F₁, на тело с площадью F₂ по отношению к полному потоку собственного излучения первого тела.

При этом φ₁₂×F₁ = φ₂₁×F₂.

Для большинства случаев, имеющих место в технике, значения угловых коэффициентов или формулы для их расчета приводятся в справочниках.

6. Теплообмен излучением между поверхностями, разделенными экраном.

Рассмотрим две поверхности разделенные экраном. Пусть Т₁ > Т₂, а степень черноты поверхностей и экрана одинакова e₁ = e₂ = e_э.

 T₁ e₁    T₂ e₂    Т_э e_э

Тепловой поток, передаваемый без крана

Тепловой поток, от первой поверхности к экрану

 Тепловой поток, от экрана ко второй поверхности

При установившемся тепловом режиме Е_1э = Е_э2, тогда

 Откуда

.С учетом последнего выражения 

Следовательно, при данных условиях, установка одного экрана уменьшает тепловой поток в два раза. Установка п экранов уменьшает тепловой поток в п – 1 раз.

В случае если e_1, e_2, e_э приведенная степень черноты определяется по формуле

Примеры решения задач:

Задача 1. Определить температуру Т, при которой энергетическая светимость Е_о черного тела равна 10 кВт/м².

Задача 2. Поток энергии Q_e, излучаемый из смотрового окошка плавильной печи, равен 34 Вт. Определить температуру Т печи, если площадь отверстия S=6 см².

Дано:                        Решение:

Задача 3. Определить энергию W, излучаемую за время t=1 мин из смотрового окошка площадью S=8 см² плавильной печи, если ее температура Т=1,2 кК.

Задачи для самостоятельного решения:

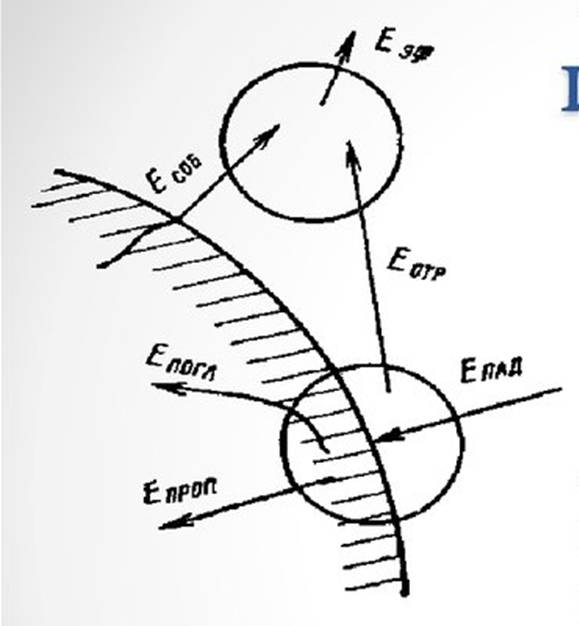
1. Чему равны степень черноты серого тела и значения E_соб при температуре T = 800 К, если E_пад = 60 кВт/м², E_погл = 48 кВт/м²?

2. Температура Т верхних слоев звезды Сириус равна 10 кК, Определить поток энергии Q_e, излучаемый с поверхности площадью S=1 км² этой звезды.

3. Определить установившуюся температуру T зачерненной металлической пластинки, расположенной перпендикулярно солнечным лучам вне земной атмосферы на среднем расстоянии от Земли до Солнца. Значение солнечной постоянной приведено в предыдущей задаче.

Домашнее задание:

Контрольные вопросы

1. Что называется теплообменом излучения

2. Какие законы теплового излучения вам известны?

3. Как осуществляется теплообмен излучением между телами.

4. Опишите теплообмен излучением между телом и оболочкой.

5. Опишите теплообмен излучением между произвольно расположенными телами.

6. Как осуществляется теплообмен излучением между поверхностями, разделенными экраном