Теплопроводность в твердом теле. Теплопередача через плоскую стенку.

1. Теплопроводность в твердом теле

Известно, что среди твердых тел различают диэлектрики и проводники тока. К последним относятся все металлы. Наряду со способностью проводить электрический ток, они одновременно обладают аномально высокой (в сравнении с диэлектриками) теплопроводностью. Установлено, что причиной этого являются свободные электроны, которые образуются в кристаллах с металлической связью. Именно они обеспечивают электропроводность и аномально высокую теплопроводность металлов.

Коэффициент электронной теплопроводности в металлах в первом приближении удается определять с помощью соотношения, подобного уже знакомому нам при анализе теплопроводности газов, а именно

v - средняя скорость теплового движения свободных электронов

 l - средняя длина свободного пробега электронов в кристаллической решетке, соизмеримая с междоузельным расстоянием; 

r - плотность электронного газа, r = п_ет_е;

п_е - концентрация свободных электронов; 

т_е -масса электрона; 

ρc_v - изохорная теплоемкость единицы объема электронного газа

Помимо электронной теплопроводности, в металлах, как и в диэлектриках, существует еще так называемая решёточная (фононная) теплопроводность.

Механизм решеточной теплопроводности имеет место во всех твердых телах. У диэлектриков он является единственным и качественно отличен от механизма электронной теплопроводности. По существу он целиком связан с особенностями теплового движения частиц, образующих кристаллическую решетку. Эти частицы не являются свободными (в отличие от электронов) и передают тепловые колебания друг другу, благодаря чему в кристалле распространяются упругие волны. Скорость этих волн (она, как мы знаем, совпадает со скоростью звука) в твёрдых телах имеет значения порядка нескольких километров в секунду. Казалось бы, с такой же скоростью должны распространяться в твердом теле и возмущения температуры. Однако реально решеточная теплопроводность λ_p сравнительно мала, обычно не превышает ~ 1 Вт/(мК), тогда как электронная теплопроводность λ_e ~ 10 ¸ 100Вт/(мК).

Причиной относительно низкой решеточной теплопроводности кристаллов является ангармоничность тепловых колебаний. Упругие волны, встречая на своём пути ангармонически колеблющиеся частицы, интенсивно рассеиваются на них и ослабляются. Рассеяние растет с повышением температуры. При этом теплопроводность кристалла уменьшается. Указанная закономерность для λ (T) в диэлектриках отчетливо наблюдается в области криогенных и низких температур. Однако в области умеренных и высоких температур решеточная теплопроводность заметно растет, что подтверждает достаточно сложный механизм явлений, определяющих теплопроводность твёрдых тел.

Теплопроводность твёрдых тел сложной макро- и микроструктуры (пористые тела, сплавы, полимеры и т. п.) зависит от многих факторов и обычно определяется с достаточной точностью только экспериментальными средствами.

Особенно низкой теплопроводностью, обладают воздушно-пористые (дисперсные) материалы. Их теплопроводность в основном определяется теплопроводностью воздуха, защемленного в многочисленных замкнутых мелких порах, и может составлять всего l ~ 0,04 ¸ 0,1 Вт/(м К).

Дисперсные полимерные материалы (пенопласты, пенополиуретаны, пенополистиролы и т.д.), наряду с разного типа войлоками и тканями, в настоящее время широко применяются в технике для тепловой изоляции разнообразных объектов. По механизму теплопроводности они близки к высокомолекулярным неэлектропроводным жидкостям.

2. Теплоёмкость твёрдых тел.

Зависимость теплоемкости твердых тел от характера термодинамического процесса проявляется только в области высоких температур. Поэтому обычно говорят просто о теплоёмкости твердых тел, не указывая особенности теплового режима.

При анализе теплоемкости кристаллической решетки тепловые колебания узлов решетки в первом приближении удается считать гармоническими. Согласно классической статистике Максвелла-Больцмана, каждый узел решетки обладает как кинетической, так и потенциальной энергией. Причем у него проявляются только три степени свободы колебательных движений, на которые приходится средняя энергия

E_кол = ikT = 3kT

Очевидно, внутренняя энергия теплового движения кристаллической решетки у 1 моля вещества составляет

U =3N_AkT = 3RT

Молярная теплоемкость кристалла, следовательно, определяется выражением

Этот результат находится в согласии с экспериментально установленным в 1819 г законом (правилом) Дюлонга и Пти, согласно которому молярная теплоёмкость всех химически чистых кристаллических твердых тел равна 3R = 25 Дж/(моль К). Этот закон хорошо оправдывается в области умеренных температур.

Однако по мере снижения температуры теплоемкость твердых тел падает и по мере приближения к абсолютному нулю температур весьма резко стремится к нулю по закону кубов Дебая, C_μ = aT³ , а = const

Причину таких резких отклонений классической теории теплоемкости твердых тел от реальной ситуации удалось объяснить только в рамках квантовой физики.

3. Теплопередача через плоскую стенку.

Простейшей и очень распространенной задачей, решаемой теорией теплообмена, является определение плотности теплового потока, передаваемого через плоскую стенку толщиной δ, на поверхностях которой поддерживаются температуры t_w1 и t_w2.

Рисунок Стационарное распределение температуры по толщине плоской стенки.

Температура изменяется только по толщине пластины - по одной координате х. Такие за­дачи называются одномерными.

Учитывая, что для одномерного случая: (1)

и используя основной закон теплопроводности, получаем дифференци­альное уравнение стационарной теплопроводности для плоской стенки:

(2)

В стационарных условиях, когда энергия не расходуется на нагрев, плотность теплового потока q неизменна по толщине стенки. В большинстве практических задач приближенно пред­полагается, что коэффициент тепло­проводности λ не зависит от температуры и одинаков по всей толщине стенки. Значение λ находят в справочниках при температуре:

(3)  средней между температурами поверхно­стей стенки.

(Погрешность расчетов при этом обычно меньше погрешности исходных данных и табличных величин, а при линейной зависимости коэффициента теплопроводности от температуры: λ = а+ bt точная расчетная формула для q не отличается от приближенной).

При λ = const:    (4)

т.е. зависимость температуры t от координаты х линейна.

Разделив переменные в уравнении (4) и проинтегрировав по t от t_w1 до t_w2 и по х от 0  

получим зависимость для расчета плотности теплового потока:

или мощность теплового потока (тепловой поток

Следовательно, количество теплоты, переданной через 1 м² стенки, прямо пропорционально коэффициенту теплопроводности λ и разности температур наружных поверхностей стенки (t_w1 – t_w2) и обратно пропорционально толщине стенки δ.

Общее количество теплоты через стенку площадью F еще и пропорционально этой площади.

Полученная простейшая формула (7) имеет очень широкое распространение в тепло­вых расчетах. По этой формуле не только рассчитывают плотности теплового потока через плоские стенки, но и делают оценки для случаев более сложных, упрощенно заменяя в расчетах стенки сложной конфигурации на плоскую стенку. Иногда уже на основании оценки тот или иной вариант отвергается без дальней­ших затрат времени на его детальную проработку.

Но формуле (7) можно рассчитать коэффициент теплопроводности материа­ла, если экспериментально измерить тепловой поток и разность температур на поверхностях пластины (стенки) известных размеров.

Температура тела в точке х определяется по формуле:

t_x = t_w1 - (t_w1 - t_w2) × (x × d)

Отношение λF/δ называется тепло­вой проводимостью стенки, а обратная величина δ/λF тепловым или термическим сопротивлением стенки и обозначается R_λ.

 Пользуясь понятием термического сопротивления, формулу для расчета теплово­го потока можно представить в виде:

(8)

Зависимость (8) аналогична закону Ома в электротехнике (сила электрического тока равна раз­ности потенциалов, деленной на электрическое сопротивление проводника, по которому течет ток).

Очень часто термическим сопротив­лением называют величину δ/λ, которая равна термическому сопротивлению плоской стенки площадью 1 м².

4. Расчет теплопередачи через многослойную стенку

Формулой формулу для расчета теплово­го потока в виде:

(1)

можно воспользоваться и для расчета теплового потока через стенку, состоя­щую из нескольких (n) плотно прилегающих друг к другу слоев разнородных материа­лов (рисунок), например, головку цилиндров, прокладку и блока цилиндров, выполненных из разных материалов, и т д.

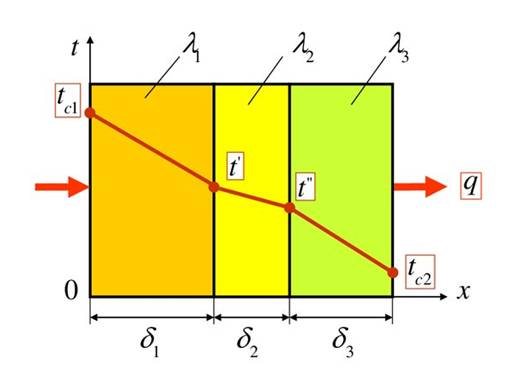
Рисунок. Распределение температуры по толщине многослойной плоской стенки.

Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоев:

  (2)

В формулу (2) нужно подставить разность температур в тех точках (по­верхностях), между которыми «включены» все суммируемые термические сопротивления, т.е. в данном случае: t_w1 и t_w(n+1):

(3)

где i – номер слоя.

При стационарном режиме удельный тепловой поток через многослойную стенку постоянен и для всех слоев одинаков.

Из (3) следует:

Из уравнения (4) следует, что общее термическое сопротивление многослойной стенки равно сумме сопротивлений каждого слоя.

Формулу (3) легко получить, записав разность температур по формуле (1) для каждого из п слоев многослой­ной стенки и сложив все п выражений с учетом того, что во всех слоях Q имеет одно и то же значение. При сложении все промежуточные температуры сократятся.

Распределение температуры в преде­лах каждого слоя — линейное, однако, в различных слоях крутизна температур­ной зависимости различна, поскольку со­гласно формуле

(dt/dx)_i = - q/λ_i.

Плотность теплового потока, проходящего через все слон, в стационарном режи­ме одинакова, а коэффициент теплопро­водности слоев различен, следовательно, более резко температура меняется в сло­ях с меньшей теплопроводностью.

Так, в примере на рисунке наименьшей теплопроводностью обладает материал второго слоя (например, прокладки), а наибольшей — третьего слоя.

Рассчитав тепловой поток через многослойную стенку, можно определить падение температуры в каждом слое по соотношению (1) и найти температуры на границах всех слоев. Это очень важно при использовании в качестве теплоизоляторов материалов с ограниченной допустимой температурой.

Температура слоев определяется по следующей формуле:

t_сл1 = t_cт1 - q × (d₁ × l₁^-1)

t_сл2 = t_cл1 - q × (d₂ × l₂^-1)

5. Контактное термическое сопротивле­ние.

При выводе формул для многослойной стенки предполагалось, что слои плотно прилегают друг к другу, и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. Идеально плотный контакт между отдельными слоями многослойной стенки получается, если одни из слоев наносят на другой слой в жидком состоянии или в виде текучего раствора. Твердые тела касаются друг друга только вершинами профилей шеро­ховатостей (рисунок).

Площадь контакта вершин пренебрежимо мала, и весь тепловой по­ток идет через воздушный зазор (h). Это создает дополнительное (контактное) термическое сопротивление R_к. Термические контактные сопротивления, могут быть определены самостоятельно с использованием соответствующих эмпирических зависимостей или экспериментально. Например, термическое сопротивление зазора в 0,03 мм примерно эквивалентно термическому сопро­тивлению слоя стали толщиной около 30 мм.

Рисунок. Изображение контактов двух шерохо­ватых поверхностей.

6. Методы снижения термического контактного сопротивления.

 Полное термическое сопротивление контакта определяется чистотой обработки, нагрузкой, теплопроводностью среды, коэффициентами теплопроводности материалов контактирующих деталей и другими факторами.

Наибольшую эффективность снижения термического сопротивления дает введение в контактную зону среды с теплопроводностью, близкой к теплопроводности металла.

Существуют следующие возможности заполнения контактной зоны веществами:

- использование прокладок из мягких металлов;

- введение в контактную зону порошкообразного вещества с хорошей тепловой проводимостью;

- введение в зону вязкого вещества с хорошей тепловой проводимостью;

- заполнение пространства между выступами шероховатостей жидким металлом.

Наилучшие результаты получены при заполнении контактной зоны расплавленным оловом. В этом случае термическое сопротивление контакта практически становится равным нулю.

Примеры решение задач.

Задача 1. Определить тепловой поток через бетонную стену здания толщиной 200 мм, высотой H = 2,5 м и длиной 2 м, если температуры на ее поверхностях: t_с1 = 20⁰С, t_с2 = - 10⁰С, а коэффициент теплопроводности λ =1 Вт/(м·К):

Задача 2. Определить коэффициент теплопроводности материала стенки толщиной 50 мм, если плотность теплового потока через нее q = 100 Вт/м², а разность температур на поверхностях Δt = 20⁰ С.

Задача 3. Плоская стенка выполнена из материала с коэффициентом теплопроводности λ= 0,25 Вт/(мК).   Толщина стенки d =50 мм. Температуры на поверхностях стенки соответственно равны: T_w1 = 50 ^оС и T_w2 = 20 ^оС. Определить плотность теплового потока через плоскую стенку.

Задача 4. Температура в плоской стенке изменяется по линейному закону Т (х) = 150 – 100х  , где х – координата, измеряемая в метрах. Толщина плоской стенки  d= 1 м. Найти плотность теплового потока через стенку. Укажите направление градиента температуры и теплового потока. Изобразите график градиента температуры по толщине плоской стенки.

Задача 5. Лед на реке толщиной  d₁ = 220 мм покрыт слоем снега толщиной d₂ = 100 мм. Температура на наружной поверхности снега Tw2 = – 10 ^оС, а на поверхности льда, обращенной к воде, Tw1 = 0 ^оС. Рассчитать плотность теплового потока.

Задача 6. Стенка сушильной камеры состоит из слоя красного кирпича толщиной  d₁ = 250 мм и слоя строительного войлока. Температуры на внутренней поверхности кирпичного слоя и на наружной поверхности войлочного слоя соответственно равны: Т_w1 = 120 ^оС и Т_w2 = 30 ^оС. Определить температуру на поверхности соприкосновения слоёв и толщину слоя войлока  d₂ при условии, что тепловые потери через 1 м² стенки камеры не должны превышать Q = 100 Вт Коэффициенты теплопроводности красного кирпича и строительного войлока принять равными λ₁ = 0,77 Вт/(мК), λ₂ = 0,05 Вт/(мК).: 

Домашнее задание

Задачи

1. Найти плотность теплового потока через плоскую стенку с термическим сопротивлением R_t = 1,75 (м² К)/Вт. Температуры на внутренней и× наружной поверхностях стенки поддерживаются равными: Т_w1 = 100 ^оС и Т_w2 = 30 ^оС.

Ответ: q = 40 Вт/м2 .

2. Определить плотность теплового потока через оконное стекло толщиной δ = 4 мм, если температуры на внутренней и наружной поверхностях стекла соответственно равны: Т_w1 = 20 ^оС и Т_w2 = 0 ^оС.

Контрольные вопросы

1. Как определить коэффициент электронной теплопроводности в металлах?

2. Что понимается под решеточной теплопроводностью?

3. Как определить тепловой поток через однослойную стенку

4. Что называется термическим сопротивлением

5. Как определить тепловой поток через многослойную стенку?