Первый закон термодинамики.

1. История открытия

Впервые этот закон был сформулирован немецким врачом и естествоиспытателем Юлиусом Робертом фон Майером. В качестве судового врача в 1840 г. он прибыл на остров Ява. Во время лечения больных ему приходилось делать кровопускание. И вот тут Майер обратил внимание на то, что венозная кровь у жителей тропиков светлее, чем у европейцев. Она была почти такой же ярко-красной, как и артериальная кровь. Учёный нашёл объяснение этому факту, предположив, что причина кроется в разнице температур между теплом собственного организма человека и теплом окружающей среды. В тропиках высокая температура, и организму требуется вырабатывать меньше теплоты. Следовательно, он сжигает меньше кислорода. Его в крови остаётся больше, и кровь переходит из артерий в вены, оставаясь практически такого же цвета. А в холодном климате организм нуждается в большем количестве тепла. И чем больше кислорода потребляет организм для этой цели, тем заметнее разница в цвете артериальной и венозной крови.

Теплоту организм получает, сжигая кислород, то есть, совершая работу. Работа превращается в теплоту. Обоснование первого закона термодинамики Майер опубликовал в 1842 г. в своей работе «Замечания о силах неживой природы». Более того, учёный нашёл и соотношение между количеством работы и количеством теплоты, полученной в результате этой работы.

Это же соотношение, независимо от Майера, экспериментально установил английский физик Джеймс Прескотт Джоуль. Результаты оказались такими же, как и у Майера. В разных экспериментах одно и то же количество работы превращалось в одно и то же количество тепла, и наоборот.

Первый закон термодинамики — это закон сохранения энергии, распространенный на тепловые явления. Он показывает, от каких причин зависит изменение внутренней энергии.

Падает, например, молот на кусок свинца, и свинец нагревается вполне определенным образом. Силы трения тормозят тела, которые при этом разогреваются.

На основании множества подобных наблюдений и обобщения опытных фактов был сформулирован закон сохранения энергии.

Энергия в природе не возникает из ничего и не исчезает: количество энергии неизменно, она только переходит из одной формы в другую.

Закон сохранения энергии управляет всеми явлениями природы и связывает их воедино. Он всегда выполняется абсолютно точно, неизвестно ни одного случая, когда бы этот великий закон не выполнялся.

В общем случае при переходе системы из одного состо­яния в другое внутренняя энергия изменяется одновремен­но как за счет совершения работы, так и за счет передачи теплоты. Первый закон термодинамики формулирует­ся именно для таких общих случаев:

Изменение внутренней энергии системы при пе­реходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, пере­данного системе:

ΔU= A + Q      (1)

Если система является изолированной, то работа внеш­них сил равна нулю (А = 0) и система не обменивается теплотой с окружающими телами (Q = 0). В этом случае согласно первому закону термодинамики ΔU = U₂ – U₁ = 0, или U₁ = U₂.

Внутренняя энергия изолированной системы остается неизменной (сохраняется).

Вместо работы А внешних тел над системой рас­сматривают работу А' системы над внешними телами. Учи­тывая, что А' = - А, первый закон термодинамики (1) можно записать так:

Q = ΔU + A'.          (2)

Количество теплоты, переданное системе, идет на изме­нение ее внутренней энергии и на совершение системой работы над внешними телами.

2. Невозможность создания вечного двигателя.

Из первого закона термодинамики вытекает невозможность создания вечного двигателя — устройства, способного совершать не­ограниченное количество работы без затрат топлива или каких-либо других материалов. Если к системе не посту­пает тепло (Q = 0), то работа А' согласно уравнению (2) может быть совершена только за счет убыли внутренней энергии: А' = —ΔU. После того как запас энергии окажется исчерпанным, двигатель перестанет работать.

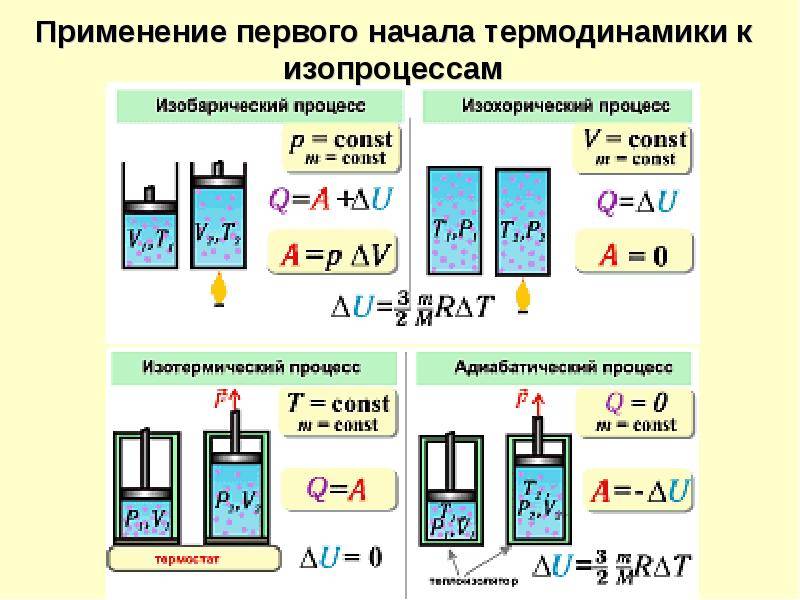
3. Применение первого закона термодинамики к различным процессам

Первый закон термодинамики имеет вид:

Q = ΔU + A'  (1)

Рассмотрим данный закон применительно к изопроцеccам.

Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.

Изохорный процесс. (V = const)

При изохорном процессе объем газа не меняется, и поэтому работа газа равна нулю A' = 0. Изме­нение внутренней энергии газа согласно уравнению (1) равно количеству переданной ему теплоты:

Физический смысл: Если газ нагревается, то Q > О и ΔU > 0, его внутренняя энергия увеличивается за счет подводимого тепла.

При охлаждении газа Q < 0 и ΔU = U₂ — U₁ < 0, изменение внутренней энергии отрица­тельно и внутренняя энергия газа уменьшается.

Изотермический процесс. (T = const)

При изотермическом процес­се (Т = const) внутренняя энергия идеального газа не меняется ΔU = 0. Согласно формуле (1) все переданное газу количество теплоты идет на совершение работы:

Q = А'.                                                                               (3)

Если газ получает тепло (Q > 0), то он совершает поло­жительную работу (А' > 0). Если, напротив, газ отдает тепло окружающей среде (термостату), то Q < 0 и А’ < 0. Работа же внешних сил над газом в последнем случае по­ложительна.

Физический смысл: При расширении получаемую газом тепло он отдает путем совершения работу, при этом его внутренняя энергия не меняется. При сжатии всю полученную путем совершения работы энергию, газ отдает путем теплообмена, при этом его внутренняя энергия не меняется.

Изобарный процесс (P = const).

При изобарном процессе согласно формуле (1) передаваемое газу количество теплоты идет на изменение его внутренней энергии и на совершение им работы при постоянном давлении:

Q = ΔU + A'  = ΔU + pΔV.  (4)

Физический смысл: Если газ нагревается: энергия получаемая газом при теплообмене,  превосходит энергию, отдаваемую путем совершения работы, что приводит к увеличению его внутренней энергии.

При охлаждении: энергия отдаваемая газом путем теплообмена, превосходит энергию, получаемую путем совершения работы, что проводит к уменьшению его внутренней энергии.

Адиабатный процесс. Рассмотрим теперь процесс, протекающий в системе, которая не обменивается теплом с окружающими телами. Процесс в теплоизолированной системе называют адиабатным.

При адиабатном процессе Q = 0 и согласно уравнению (1) изменение внутренней энергии происходит только за счет совершения работы:

ΔU = - А'.        (5)

Конечно, нельзя окружить систему оболочкой, абсолютно не допускающей теплопередачу. Но в ряде случаев можно считать реальные процессы очень близкими к адиабатным. Для этого они должны протекать достаточно быстро, так, чтобы за время процесса не произошло заметного теплообмена между системой и окружающими телами.

Физический смысл: При расширении газ отдает энергию путем совершения работы, при этом его внутренняя энергия уменьшается. При сжатии вся энергия, полученная газом путем совершения над ним работы, идет на увеличение его внутренней энергии.

При адиабатном процессе работа

 , 

где γ – показатель адиабаты

Уравнение Пуассона (Уравнение газового состояния gри адиабатном процессе) pV^γ=const

связь между начальным и конечным значениями параметров состояний газа при адиабатном процессе:

Примеры решения задач:

Задача 1. Водород массой m = 0,66 кг изобарно нагрели на ΔТ =328К. Найти

1) работу А, совершенную газам;

2) количество теплоты Q, сообщенное газу;

3) изменение внутренней энергии

Задача 2.  Кислород массой m=2 кг занимает объем V₁=1 м³ и находится под давлением p₁=0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂=3 м³, а затем при постоянном объеме до давления p₃=0,5 МПа. Найти:
1) изменение внутренней энергии ΔU газа;
2) совершенную им работу A;
3) количество теплоты Q, переданное газу. Построить график процесса.

Задача 3. Азот массой m=2 г, имевший температуру T₁=300 К, был адиабатно сжат так, что его объем уменьшился в n=10 раз. Определить конечную температуру T₂ газа и работу A сжатия

Задача 4. Баллон вместимостью V=20 л содержит водород при температуре T= 300 К под давлением p=0,4 МПа. Каковы будут температура T₁ и давление p₁, если газу сообщить количество теплоты Q=6 кДж?

Дано:

V=20 л

T= 300 К

p=0,4 МПа

Q=6 кДж

T₁ - ?

 p₁ -?

Решение:

Задача 5. Азот нагревался при постоянном давлении, причем ему было сообщено количество теплоты Q=21 кДж. Определить работу A, которую совершил при этом газ, и изменение ΔU его внутренней энергии.

Задача 6. С одноатомным идеальном газом проводят циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя? Количество вещества газа в ходе процесса остаётся неизменным.

Задачи для самостоятельного решения:

1. Газ массой m изобарно нагрели на ΔТ. Найти 1) работу А, совершенную газам; 2) количество теплоты Q, сообщенное газу; 3) изменение внутренней энергии

 2. Для изобарного нагревания газа, количество вещества которого 800 моль, на 500 К ему сообщили количество теплоты 9,4 МДж. Определить работу газа и приращение его внутренней энергии.

3. Удельная теплоемкость азота, когда его нагревают при постоянном давлении, равна 1,05 кДж/(кг • К), а при постоянном объеме — 0,75 кДж/(кг • К). Почему эти величины имеют разные значения? Какая совершается работа при изобарном нагревании азота массой 1 кг на 1 К?

4. Идеальный газ получил количество теплоты, равное 300 Дж, и совершил работу, равную 100 Дж. Как изменилась внутренняя энергия газа?

А. увеличилась на 400 Дж

 Б. увеличилась на 200 Дж

 В. уменьшилась на 400 Дж

 Г. уменьшилась на 200 Дж

5. Идеальный газ совершил работу, равную 100 Дж, и отдал количество теплоты, равное 300 Дж. Как при этом изменилась внутренняя энергия?

А. увеличилась на 400 Дж

 Б. увеличилась на 200 Дж

 В. уменьшилась на 400 Дж

 Г. уменьшилась на 200 Дж

6. Идеальный газ совершил работу, равную 300 Дж. При этом внутренняя энергия уменьшилась на 300 Дж. Каково значение количества в этом процессе?

А. отдал 600 Дж

 Б. отдал 300 Дж

 В. получил 300 Дж

 Г. не отдавал и не получал теплоты.

7. Идеальный газ совершил работу, равную 300 Дж. При этом его внутренняя энергия увеличилась на 300 Дж. Какое количество теплоты получил газ?

А. отдал 600 Дж

 Б. отдал 300 Дж

 В. получил 600 Дж

 Г. получил 300 Дж

8. Объем кислорода массой 160 г, температура кото­рого 27 °С, при изобарном нагревании увеличился вдвое. Найти работу газа при расширении, количество теплоты, которое пошло на нагревание кислорода, изменение внутренней энергии.

Домашнее задание:

Задачи:

1. При адиабатическом сжатии газ совершил работу 200Дж.Как и насколько изменилась при этом внутренняя энергия?

2. Вычислить увеличение внутренней энергии водорода массой 2кг при изохорном повышении температуры на 10 К.

3. Объем кислорода массой 160 г, температура которого 27 °С, при изобарном нагревании увеличился вдвое. Найти работу газа при расширении, количество теплоты, которое пошло на нагревание кислорода, изменение внутренней энергии.

4. Одноатомный идеальный газ в количестве 10 моль сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2–3?

5. Во сколько раз количество теплоты, которое идет на нагревание газа при постоянном давлении, больше работы, совершаемой газом при расширении? Удельная теплоемкость газа при постоянном давлении с_р, молярная масса М.

Контрольные вопросы:

1. В каком случае работа газа больше: при изотермическом расширении от объема V₁, до объема V₂ или при изобарном расширении от объема V₁, до объема V₂&

2. Как следует записать уравнение теплового баланса для изолированной системы из трех тел, переходящей в равновесное состояние.

3. Как формулируется первый закон термодинамики?

4. В каком случае изменение внутренней энергии отрицательно?

5. Почему можно говорить, что система обладает внутренней энергией, но нельзя сказать, что она обладает запасом определенного количества теплоты или работы?