Движение тела по окружности с постоянной по модулю скоростью

Одним из видов механического движения является криволинейное движение. В криволинейному равномерному движению относится движение тела по окружности.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

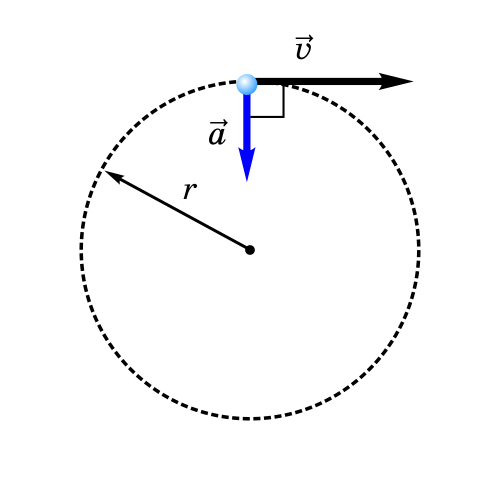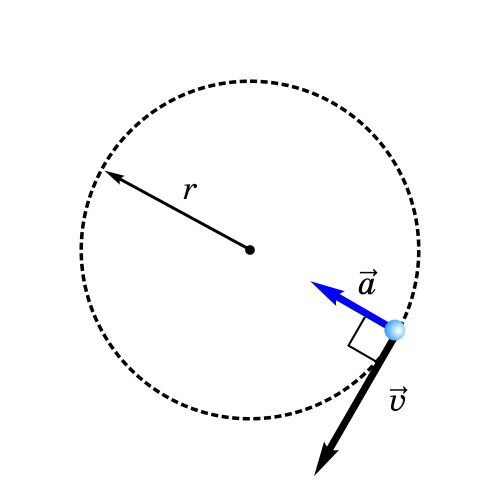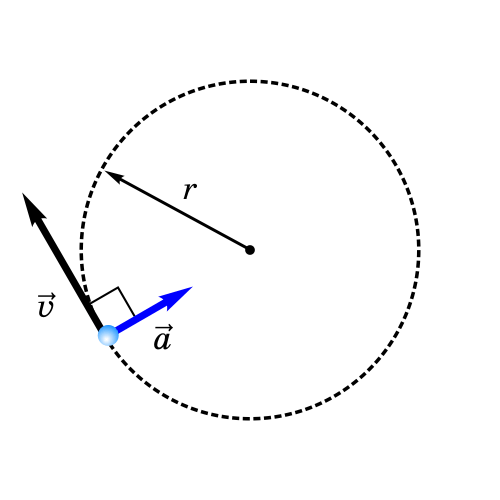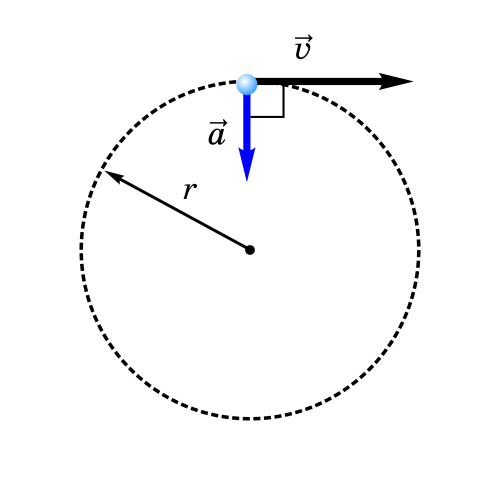
Вектор скорость всегда касательный к траектории движения

Положение тела на окружности определяется радиусом-вектором, проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

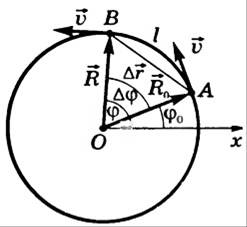
Рис. 1

За время Δt тело, двигаясь из точки А в точку В, совершает перемещение  , равное хорде АВ, и проходит путь, равный длине дуги l.

Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.

Скорость   движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена: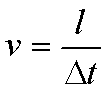       

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью.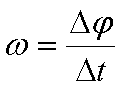   

В СИ единицей угловой скорости является радиан в секунду (рад/с).

Связь между линейной и угловой скоростью.

Учитывая, что  , получаем           ⇒  υ=ωR — формула связи между линейной и угловой скоростью.

Кинематическое уравнение движения материальной точки по окружности:

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.

Положение тела можно определить, если известен модуль радиуса-вектора  и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t₀ = 0 угловая координата равна φ₀, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время  Δt = t−t₀ = t равен  Δφ = φ−φ₀. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности: φ = φ₀ + ωt.

Оно позволяет определить положение тела в любой момент времени t.

Ускорение при равномерном движении тела по окружности

При равномерном движении тела по окружности величины v и ω остаются неизменными. В этом случае при движении изменяется только направление вектора . 

Равномерное движение тела по окружности является движением с ускорением. Ускорение    направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями: 

Вывод формулы ускорения тела по окружности.

Для доказательства этого выражения рассмотрим изменение вектора скорости  за малый промежуток времени Δt. По определению ускорения

Векторы скоростей  и  в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы v_A = v_B = v. Из подобия треугольников OAB и BCD следует:

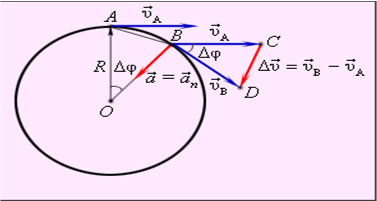
      Рисунок 2.

При малых значениях угла Δφ = ωΔt расстояние |AB| =Δs ≈ vΔt. Так как |OA| = R и |CD| = Δv, из подобия треугольников на рис.2 получаем:

При малых углах Δφ направление вектора  приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0, получим:

Направление ускорения тела, движущегося по окружности

При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.

При равномерном движении тела по окружности вектор ускорения все время перпендикулярен вектору скорости, который направлен по касательной к окружности.

 

     

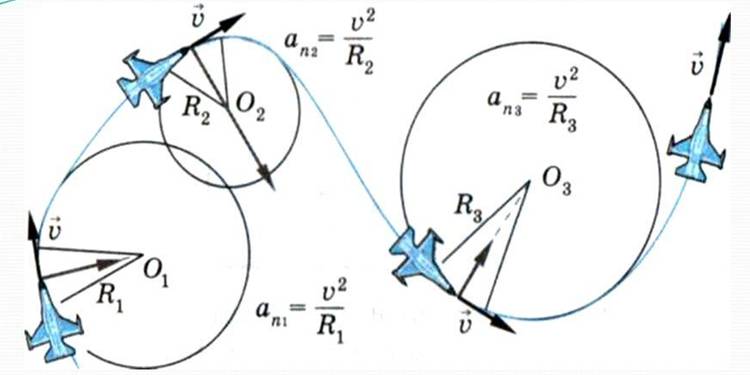
В векторной форме центростремительное ускорение может быть записано в виде