Уравнение прямолинейного равноускоренного движения.

Ускорение. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением. Ускорением называется векторная величина, равная отношению очень малого изменения вектора скорости к малому промежутку времени Δt , за которое произошло это изменение:   .  (1)

Самый простой вид неравномерного движения — это равноускоренное движение.

Скорость равноускоренного движения. При равноускоренном движении с начальной скоростью ускорение равно , (2)

Отсюда скорость равноускоренного движения равна . (3)

Проекции скорости и ускорения. Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.

Векторы начальной скорости и ускорения могут иметь различные направления, поэтому переход от уравнения (3) в векторной форме к уравнениям в алгебраической форме может оказаться довольно сложной задачей. Задача нахождения модуля и направления скорости равноускоренного движения в любой момент времени может быть успешно решена следующим путем. Как известно, проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось. Поэтому для нахождения проекции v_х вектора скорости на произвольную ось ОХ нужно найти алгебраическую сумму проекций векторов и на ту же ось: . (4)

Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной — в противоположном случае.

Так, в случае расположения векторов и , представленном на рисунке 1, их проекции и на ось ОХ положительны. В случае расположения векторов и , представленном на рисунке 2, проекция положительна, а проекция отрицательна.

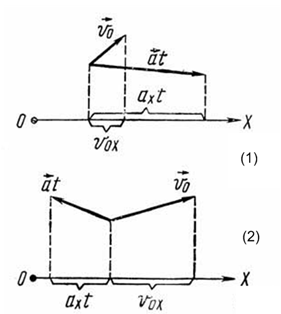
График скорости. Из уравнения (4) следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось ОХ равна нулю ( = 0), то эта прямая проходит через начало координат (рис 3).

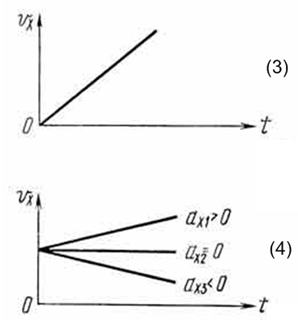
Графики зависимости проекции скорости от времени t для равноускоренных движений, происходящих с одинаковой начальной скоростью и различным ускорением , приведены на рисунке 4.

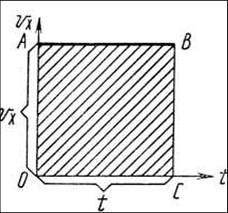
Перемещение тела при равномерном движении. Установим связь проекции S_x вектора перемещения на координатную ось ОХ при равномерном прямолинейном движении с проекцией вектора скорости v_x на ту же ось и временем t.

   При равномерном прямолинейном движении график зависимости проекции скорости v_x от времени t является прямой, параллельной оси абсцисс (рис. 5).

(5)

Проекция S_x перемещения тела за время t при равномерном движении со скоростью v определяется выражением      .

Длина стороны ОА прямоугольника ОАВС (рис.5) пропорциональна проекции скорости v_x, длина стороны ОС — времени движения t. Следовательно, площадь прямоугольника ОАВС прямо пропорциональна произведению или проекции перемещения S_x.

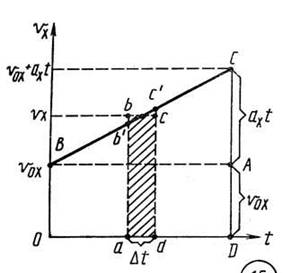
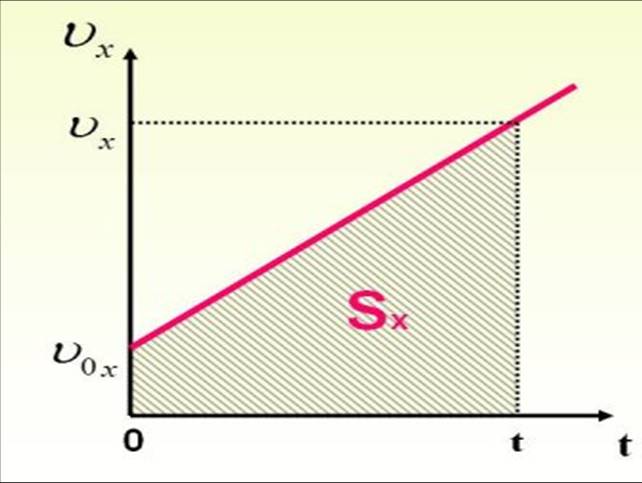
Перемещение тела при равноускоренном прямолинейном движении. График зависимости проекции v_x скорости тела от времени при равноускоренном прямолинейном движении представлен на рисунке 6.

(6)

Для вычисления проекции перемещения тела при равноускоренном прямолинейном движении за время t найдем сначала перемещение за малый промежуток времени Δt.

Если промежуток времени Δt очень мал, то и изменение скорости за этот промежуток времени очень мало, т. е. движение в течение этого промежутка времени можно считать равномерным. При равномерном движении со скоростью, равной мгновенной скорости в момент времени, определяемый серединой промежутка времени Δt, проекция перемещения ΔS_x за промежуток времени Δt равна ΔS_x= v_xΔt и пропорциональна площади прямоугольника abcd. Площадь прямоугольника abcd равна площади трапеции ab'c'd.

Разбив промежуток времени 0 до t на малые промежутки времени Δt, мы получим, что проекция перемещения при равноускоренном прямолинейном движении за время t пропорциональна площади трапеции OBCD. Трапецию OBCD можно представить состоящей из прямоугольника OBAD и прямоугольного треугольника ABC. Сумма их площадей равна     .

Отсюда для проекции перемещения при равноускоренном прямолинейном движении получается выражение  . (5)

Уравнение для координаты точки при равноускоренном движении. Для нахождения координаты x точки в любой момент времени t нужно к начальной координате х₀ точки прибавить проекцию вектора перемещения на ось ОХ (рис. 7):     х=х₀+ S_х..(6)

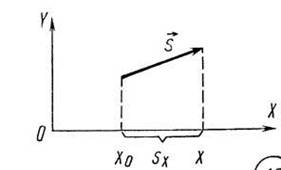(7)

Из выражений (6) и (5) следует:    .(7)

Связь проекции перемещения тела с конечной скоростью при равноускоренном движении. Из уравнений (4) и (5) можно получить уравнение, связывающее проекции конечной скорости v_x, начальной скорости v_0x и ускорения а_х с проекцией перемещения тела S_x:       . (8)

В случае равенства проекции начальной скорости нулю получаем выражение

        . (9)

Из этого выражения можно найти проекции скорости  v_x или ускорения а_х по известному значению проекции перемещения :  , (10)    . (11)

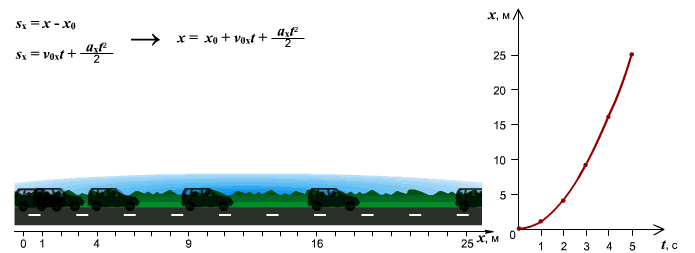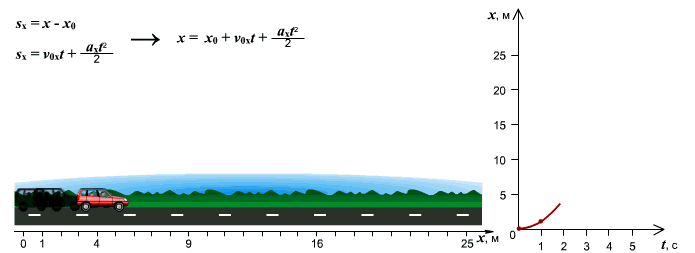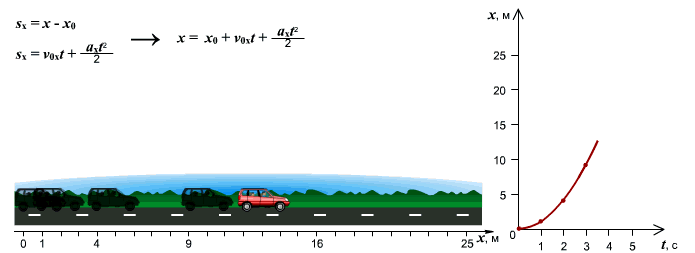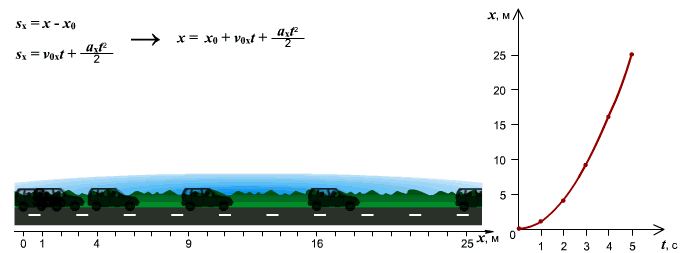
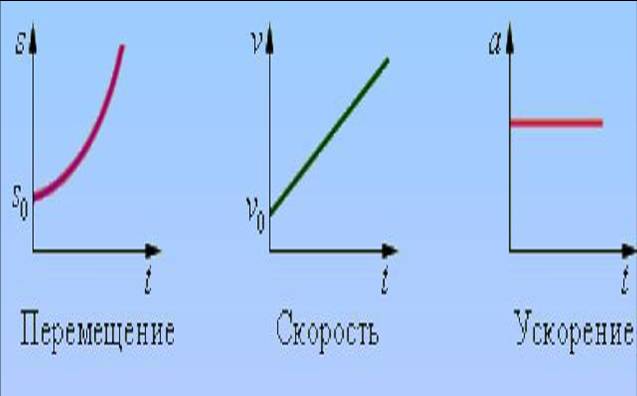
Графики перемещения, скорости, ускорения при равноускоренном движении тела.

Контрольные вопросы:

1. Запишите формулы прямолинейного равномерного движения для скорости и пройденного пути.

2. Запишите формулы равноускоренного прямолинейного движения для скорости и пройденного пути.

3. Постройте графики зависимости проекции скорости, перемещения тела от времени при равноускоренном (равнозамедленном) прямолинейном движении

Пример решения задач

Задача. Теплоход, двигаясь равноускоренно из состояния покоя с ускорением 0,1 м/с², достигает скорости 18 км/ч, за время 20с. Какой путь за это время пройден?

Задачи для самостоятельного решения:

1. Первый вагон трогающегося от остановки поезда прохо­дит за 3 с мимо наблюдателя, находившегося до отправления поезда у начала этого вагона. За сколько времени пройдет мимо наблюдателя весь поезд, состоящий из 9 вагонов? Про­межутками между вагонами пренебречь.

2. Зависимость скорости материальной точки от време­ни задана формулой v_x = 6t. Написать уравнение х = x(t), если в начальный момент (t = 0) движущаяся точка находилась в начале координат (х = 0). Вычислить путь, пройденный мате­риальной точкой за 10 с.

3. Участок пути длинной 1 км мотоциклист, двигаясь из состояния покоя, проходит с постоянным ускорением 0,8 м/с². За какое время это путь пройден? Какова скорость в конце данного участка цели?

4. Самолет для взлета должен приобрести скорость 250 км/ч. Сколько времени длится разгон, если эта скорость достигнута в конце взлетной полосы длиной 1 км? Каково ускорение самолета? Движение самолета считать равноускоренным.

5. Первый автомобиль движется равномерно со скоростью 57,6 км/ч. В момент прохождения им пункта А, из этого пункта начинает двигаться второй автомобиль по тому же направлению с постоянным ускорением 2 м/с². Через какое время второй автомобиль догонит первый? На каком расстоянии от пункта это произойдет? Какова будет скорость второго  автомобиля в этот момент?

6. При какой посадочной скорости самолеты могут приземляться на посадочной полосе аэродрома 800м при торможении с а₁=-2,7 м/с²? а₂=-5 м/с²?

7. Поезд, двигаясь под уклон, прошел за 20 с путь 34о м и развил скорость 19 м/с. С каким ускорением двигался поезд и какой была скорость в начале уклона?

Домашнее задание:

Задачи:

1.Два мотоциклиста выезжают одновременно из двух пунк­тов навстречу друг другу. Один из них спускается равноускоренно с горы, имея начальную скорость 36 км/ч и ускорение 2 м/с². Другой равнозамедленно поднимается в гору с начальной скоростью 72 км/ч и с тем же по модулю ускорением. Первоначальное расстояние между мотоциклистами равно 300 м. Через сколько времени они встретятся?

 2. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь.

Составить таблицу