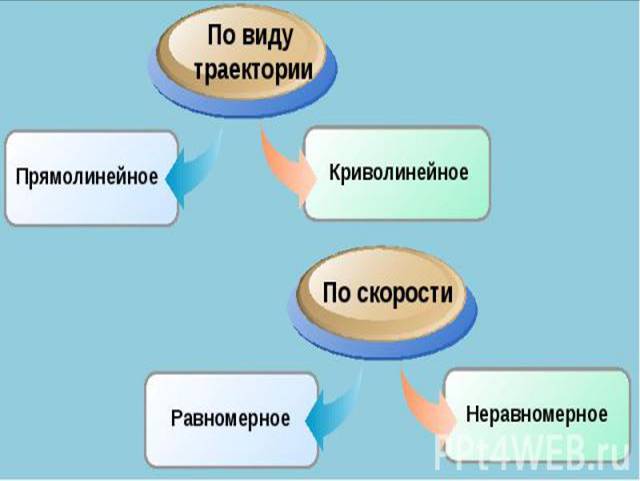
Характеристики механического движения
Виды движения:

Движение
тела (точки) называется равномерным, если оно за любые равные промежутки времени
проходит одинаковые пути.
Равномерное движение может быть как криволинейным, так и прямолинейным.
Равномерное прямолинейное движение — самый простой вид движения.
Важной величиной, характеризующей движение тела, является его скорость.
Некоторое представление о скорости каждый из нас имел и до начала изучения
физики. Черепаха перемещается с малой скоростью, человек движется с большей
скоростью, автомобиль движется быстрее человека, а самолет — еще быстрее. Самой
большой скорости относительно Земли человек достигает с помощью космических
ракет.
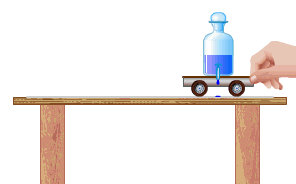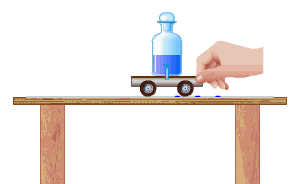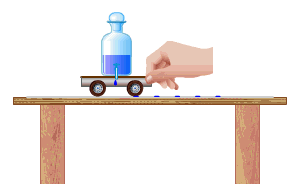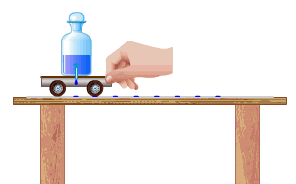
Скоростью
равномерного прямолинейного движения тела называется величина, равная отношению
его перемещения к промежутку времени, в течение которого это перемещение
произошло.
(1)
![]()
Получим
уравнение равномерного прямолинейного движения точки. Для этого воспользуемся
определением скорости. Пусть радиус-вектор г0 задает положение точки
в начальный момент времени
t0,
а радиус-вектор г — в момент времени
t. Тогда
![]() (2)
(2)
Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.
Вместо векторного уравнения можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор г является суммой двух векторов: радиус-вектора г0 и вектора vt. Следовательно, проекции радиус-вектора г на оси координат должны быть равны сумме проекций этих двух векторов на те же оси.
Выберем оси координат так, чтобы тело двигалось по какой-либо оси, например по оси ОХ. Тогда векторы г0 и v будут составлять с осями OY и OZ прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора г на оси OY и OZ. Так как проекции радиус-вектора на координатные оси равны координатам его конца, то гх = х и г0х =х0. Поэтому в проекциях на ось ОХ уравнение (2) можно записать в виде х = х0 + vxt. (3)
Уравнение (3) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.
Учитывая формулу (1) запишем формулы, определяющие положение тела при его движении по прямой и по плоскости.
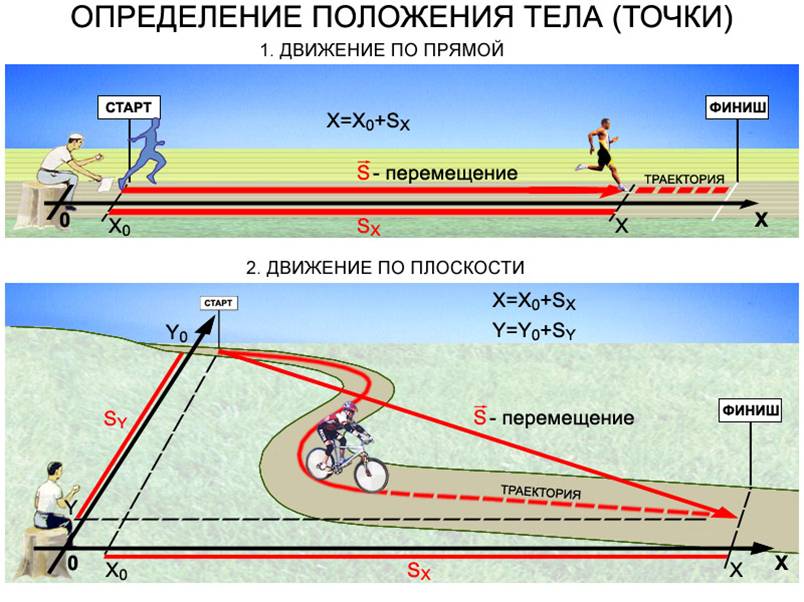
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.
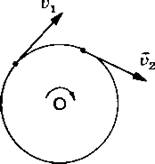
Так, скорость шайбы, скользящей по льду, уменьшается с течением времени до полной ее остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис. 1)
Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению (рис 2).
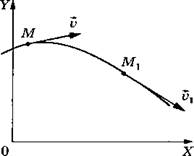
Чтобы полностью описать неравномерное движение точки, надо знать ее положение и скорость в каждый момент времени. Скорость в данный момент времени называется мгновенной скоростью.
Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени.
Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости: ускорение.
Ускорение – это величина характеризующая быстроту изменения скорости.
Движение с ускорением можно разделить на два вида: движение с постоянным ускорением, когда модуль и направление вектора ускорения не меняются со временем, и движение с переменным ускорением, когда ускорение со временем меняется.
Движение с постоянным ускорением является наиболее простым движением с переменной скоростью. Можно приближенно считать, что с постоянным ускорением движется автобус (или поезд) при отправлении в путь и при торможении, скользящая по льду шайба и т. д.

Если
ускорение тела постоянно, то отношение изменения скорости к интервалу времени,
за которое это изменение произошло, будет одним и тем же для любого интервала
времени. Поэтому, обозначив через ∆t некоторый произвольный промежуток времени,
а через ∆v — изменение скорости за этот промежуток, можно записать:
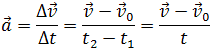
Ускорением тела при его равноускоренном движении называют постоянную векторную величину, равную отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло.
Ускорение тела нужно знать, чтобы вычислить мгновенную скорость тела.
Прямолинейное движение с постоянным ускорением, при котором модуль скорости увеличивается, называется равноускоренным движением, а прямолинейное движение с постоянным ускорением, при котором модуль скорости уменьшается, называется равнозамедленным.
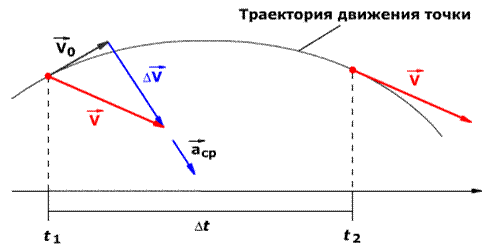
Если за промежуток
времени Δt тело из точки А траектории переместилось в точку В
и его скорость изменилась от
![]() до
до
![]() ,
то изменение скорости
,
то изменение скорости
![]() за
этот промежуток времени равно разности векторов
за
этот промежуток времени равно разности векторов
![]() и
и
![]() :
: ![]()
Направление вектора
ускорения а совпадает
с направлением вектора изменения скорости
![]() при
очень малых значениях промежутка времени Δt , за который происходит
изменение скорости.
при
очень малых значениях промежутка времени Δt , за который происходит
изменение скорости.
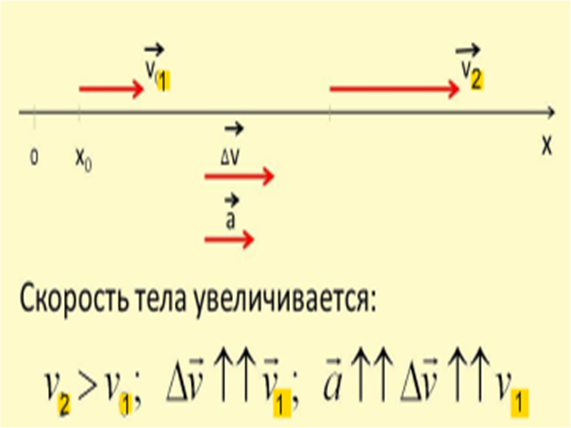
Если тело движется
прямолинейно и скорость его возрастает по модулю,
то направление вектора ускорения совпадает с направлением вектора скорости
![]() ; при убывании
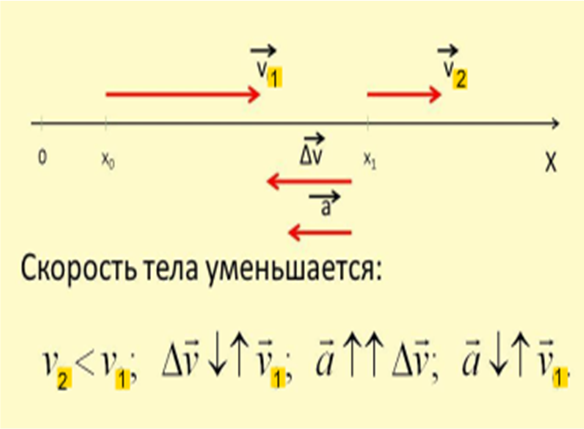
скорости по модулю,
направление вектора ускорения противоположно направлению вектора скорости
; при убывании
скорости по модулю,
направление вектора ускорения противоположно направлению вектора скорости
![]() .
.
При движении тела по
криволинейной траектории направление вектора скорости изменяется в процессе
движения, вектор ускорения а при
этом может оказаться направлен под любым углом к вектору скорости
![]() .
.
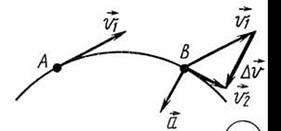
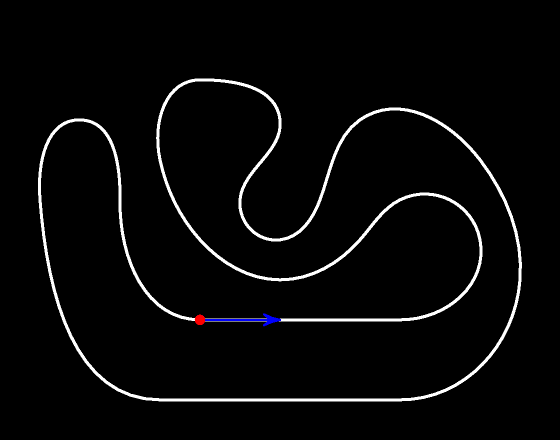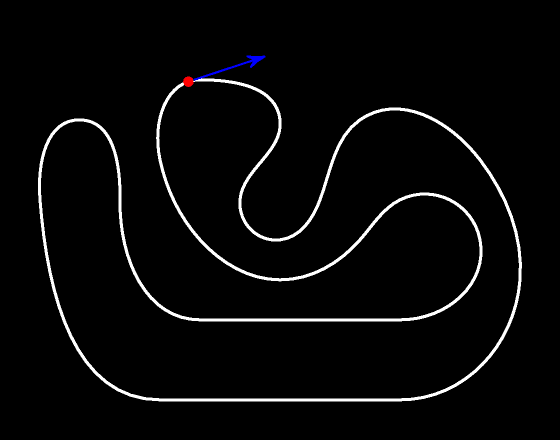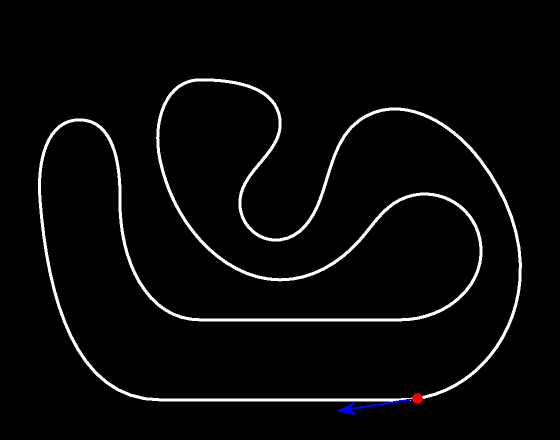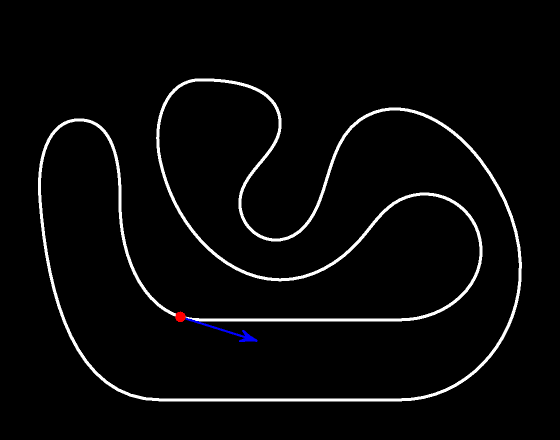
Вектор скорость всегда касательный к траектории движения
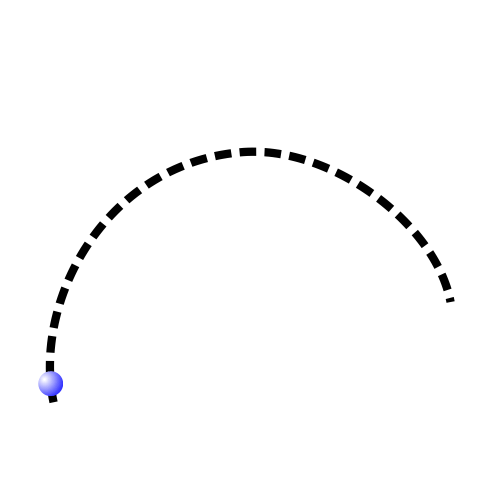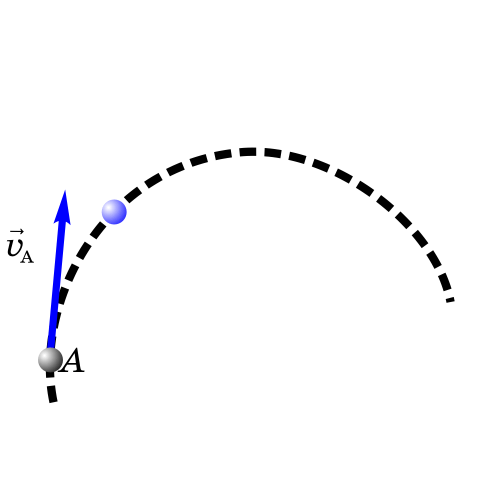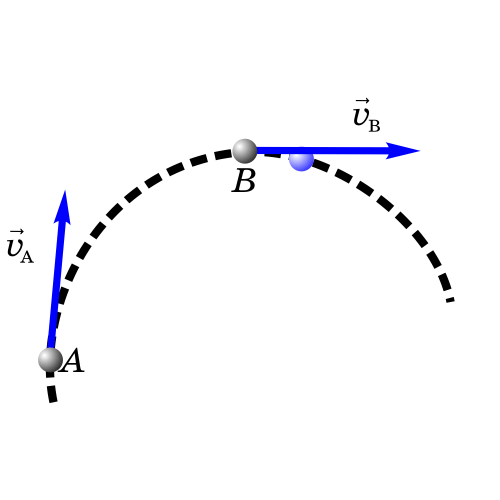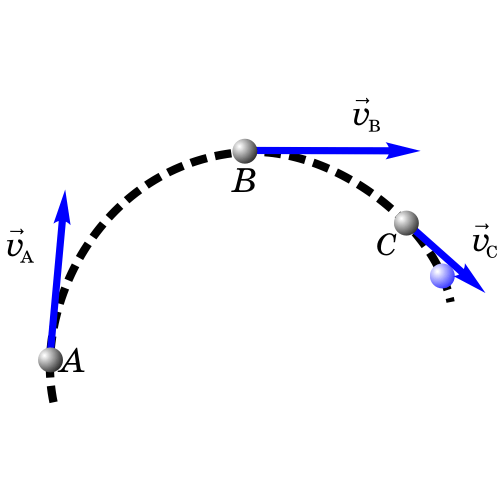
Равноускоренным
называется движение с ускорением, постоянным по модулю и направлению:
![]() .
.
Из формулы следует, что при выражении скорости в метрах в секунду, а времени в секундах ускорение выражается в метрах на секунду в квадрате:
![]() .
.
Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки изменяется на 1 м/с.
Скорость
равноускоренного движения.
При равноускоренном движении с начальной скоростью
![]() ускорение а равно
ускорение а равно
![]() .
.
Отсюда скорость равноускоренного движения
равна ![]() .
.
В проекциях на ось Ох получим: vx = v0x + axt
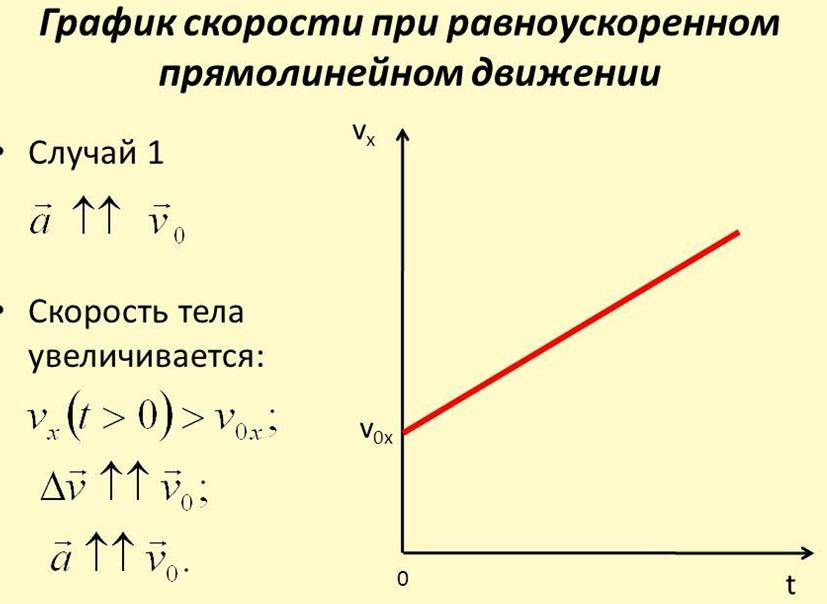

Вопросы:
1. При любом неравномерном движении
изменяется скорость. Как ускорение характеризует это изменение?
2. Чем отличается «замедленное»
прямолинейное движении от «ускоренного»?
Примеры решения задач:
Задача 1. Мотоциклист начинает движение из состояния покоя. Через 40 с он достигает скорости 20 м/с. С каким ускорением происходит движение?
Задача 2. Ускорение лыжника на одном из спусков трассы равно 2,4 м/с2. На этом спуске его скорость увеличивается на 36 м/с. Время, затраченное лыжником на спуск, равно
Задачи для самостоятельного решения:
1. Скорость поезда за 20 с уменьшилась с 72 до 54 км/ч. Написать формулу зависимости скорости от времени ux(t) и построить график этой зависимости.
2. Поезд через 10 с после начала движения приобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с?
3. По дороге навстречу друг другу движутся два автомобиля: один со скоростью 60 км/ч, другой 90 км/ч. У заправочной станции автомобили встретились и после этого продолжили свой путь. Определить положение каждого автомобиля через 30 мин после встречи и расстояние между ними в этот момент.
4. Два автомобиля движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. В некоторый момент времени первый автомобиль, движущийся со скоростью 20 км/ч, находился на расстоянии 200м от перекрестка. Второй автомобиль в тот же момент находился на расстоянии 300 км от перекрестка. С какой скоростью двигался второй автомобиль, если оба автомобиля подъезжают к перекрестку одновременно.
5. Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью 10 м/с. В этот момент времени водитель нажимает на тормоз и автомобиль начинает двигаться с ускорением 1м/с2 . Сколько времени пройдет до остановки автомобиля?
6. Тело движется с постоянно уменьшающейся скоростью. Ускорение постоянно и равно 4м/с2 . В некоторый момент времени модуль скорости тела 20 м/с. Найти скорость тела через 4с и 8с после этого момента.
Домашнее задание:
Задачи:
1. Тело движется вдоль координатной оси ОХ. Направления начальной скорости и ускорения совпадают с положительным направлением оси, а их модули равны v0 = 4 м/с, а = 2 м/с2. Определите скорость через 4 с от начала отсчета времени.
2. В точке с координатой х0= 10 м тело имело скорость v0 = 20 м/с, направленную противоположно положительному направлению оси ОХ. Ускорение тела направлено противоположно вектору начальной скорости, а его модуль равен 10 м/с2. Определите координату тела в моменты времени 1, 2, 3, 4 с от начала отсчета.
Контрольные вопросы:
1. Как записывается в
векторной форме уравнение равномерного прямолинейного движения точки?
2. Как записывается в координатной форме уравнение равномерного
прямолинейного движения точки, если она движется: по оси Оу, по оси Oz,
3. Что называется ускорением тела? В каком случае ускорение тела
считается постоянным?
4. Куда направлено ускорение тела при его равноускоренном движении тела?
при равнозамедленном движении?
5. В каких единицах измеряется модуль ускорения?
6. Какие виды движения вы знаете?
7. В каких единицах измеряется модуль ускорения?
8. Запишите формулу для определения скорости тела при его равноускоренном
движении в векторном виде (в проекциях на ось х)?
9. Куда направлено ускорение тела при его равноускоренном движении тела?
при равнозамедленном движении?
10. Нарисуйте график скорости при равноускоренном движении тела.
Составить план обобщенного характера изучения величины – скорость, ускорение.
Пункты плана
1. Какое явление и свойство тел (веществ) характеризует данная величина.
2. Определение величины.
3. Определительная формула (для производной величины – формула, выражающая связь
данной величины с другими).
4. Какая величина – скалярная или векторная.
5. Единица величины в СИ.
6. Способы измерения величины