Работа в термодинамике
Понятие – работа в термодинамике
В результате каких процессов может меняться внутренняя энергия? Есть два вида таких процессов: совершение работы и теплопередача. Начнем с работы. Чему она равна при сжатии и расширении газа и других тел?
В механике работа определяется как произведение модуля силы, модуля перемещения точки ее приложения и косинуса угла между ними. При действии силы на движущееся тело работа равна изменению его кинетической энергии.
В термодинамике движение тела как целого не рассматривается, речь идет о перемещении частей макроскопического тела друг относительно друга. В результате может меняться объем тела, а его скорость остается равной нулю.

Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии.
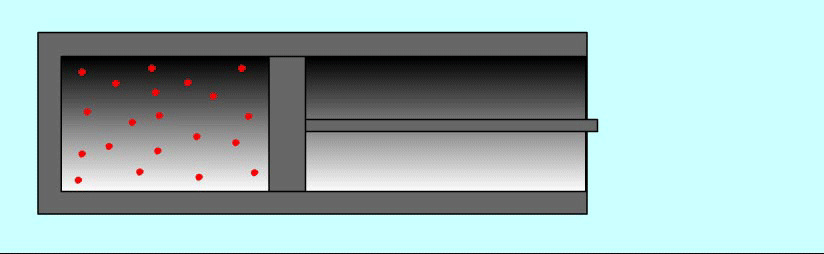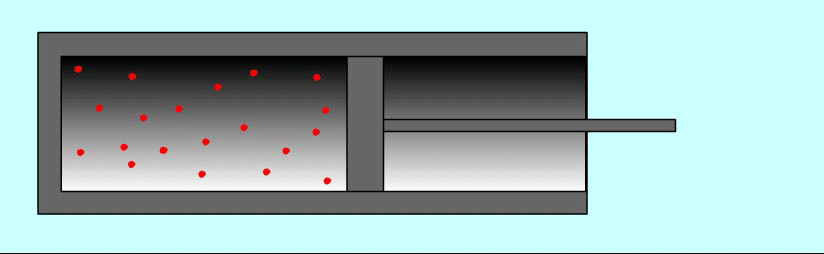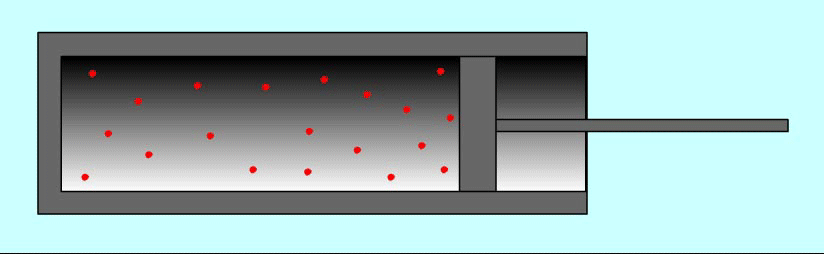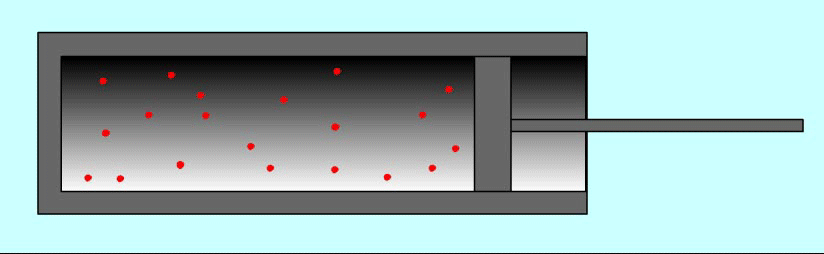
Почему при сжатии или расширении тела меняется его внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?
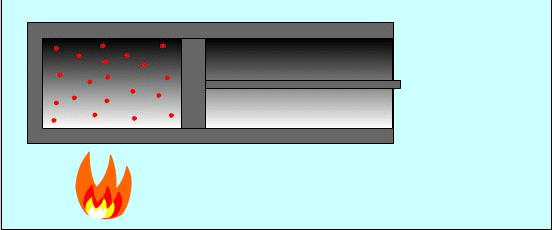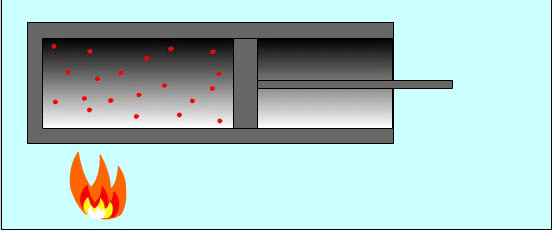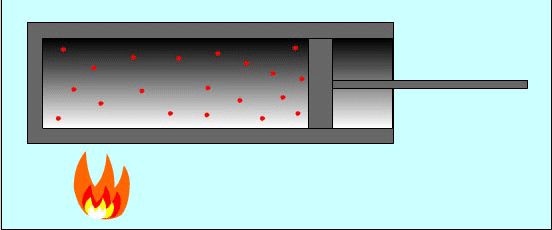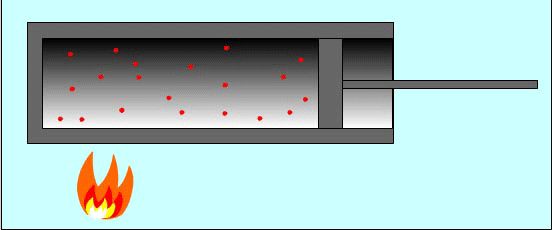
Причина изменения температуры газа в процессе его сжатия состоит в следующем: при упругих соударениях молекул газа с движущимся поршнем изменяется их кинетическая энергия. Так, при движении навстречу молекулам газа поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги. Нога сообщает мячу скорость, значительно большую той, которой он обладал до удара.
И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, — нога футболиста движется от мяча, как бы уступая ему дорогу.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
Вычисление работы.
Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем. Проще всего вначале вычислить не работу силы F, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой F'.
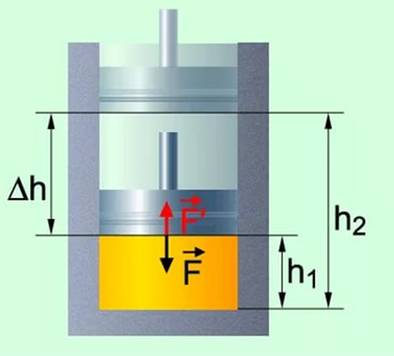
Согласно третьему закону Ньютона F = - F'.
Модуль силы, действующей со стороны газа на поршень, равен F' = pS,
где р — давление газа, a S — площадь поверхности поршня.
Пусть газ расширяется изобарно и поршень смещается в направлении силы F' на малое расстояние Δh = h2 – h1.
Так как давление газа постоянно, то работа газа равна:
А' = F'Δh = pS (h2 -h1)=p (Sh2 – Sh1).
Эту работу можно выразить через изменение объема газа. Начальный его объем V1 = Sh1, а конечный V2 = Sh2.
Поэтому А' = р (V2 – V1) = pΔV (1),
где ΔV = V2 – V1.
При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают.
Если газ сжимается, то формула (1) для работы газа остается справедливой. Но теперь V2 < V1 и поэтому А' < О.
Работа А, совершаемая внешними телами над газом, отличается от работы самого газа А' только знаком: А = -А', так как сила F, действующая на газ, направлена против силы F', а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:
А = -А' = -рΔV
При изобарном процессе работа, совершенная газом при его расширении, равна A = p(V2 – V1).
Полученное уравнение позволяет выявить физический смысл универсальной газовой постоянной R.
Запишем
для двух состояний газа уравнение Менделеева–Клапейрона:
pV2 = νRT2,
pV1 = νRT1.
Вычитая из первого уравнения второе, имеем: p(V2 – V1) = νR(T2 – T1).
Как было получено выше, p(V2 – V1) = А.
Таким образом: А = νR(T2 – T1).
Выразим из полученного уравнения R: 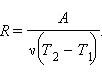
Если ν = 1 моль, T2 – T1 = 1 K, то R = A.
Таким образом, универсальная газовая постоянная – это физическая величина, численно равная работе, совершенной 1 молем идеального газа при его изобарном расширении в результате повышения температуры на 1 К.
Работа газа при расширении
Геометрическое истолкование работы.
Работе А' газа для случая постоянного давления можно дать простое геометрическое истолкование.
Построим график зависимости давления газа от занимаемого им объема (рис. 1).
Здесь площадь прямоугольника abdc, ограниченная графиком р = const, осью V и отрезками аb и cd, равными давлению газа, численно равна работе:
A'=P1 (V2 – V1) = |аb | · |ас|.
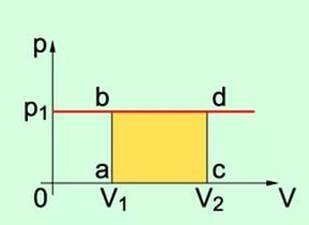
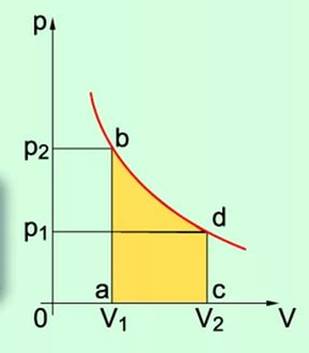
Рисунок 1 Рисунок 2
В общем случае давление газа не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 2). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости р от V, осью V и отрезками аb и cd, равными давлениям р1, р2 в начальном и конечном состояниях газа.
Таким образом, работа, совершаемая газом а процессе его расширения (или сжатия) при любом термодинамическом процессе, численно равна площади под кривой, изображающей изменение состояния газа на диаграмме (р,V).
Задание: Составить план обобщенного характера изучения величины работа.
1. Какое явление и свойство тел (веществ) характеризует данная величина.
2. Определение величины.
3. Определительная формула (для производной величины – формула, выражающая связь данной величины с другими).
4. Какая величина – скалярная или векторная.
5. Единица величины в СИ.
6. Способы измерения величины
Примеры решения задач:
Задача 1. В вертикально расположенном цилиндре с площадью основания 1 дм2 под поршнем массой 10 кг, скользящим без трения, находится воздух. При изобарном нагревании воздуха поршень поднялся на 20 см. Какую работу совершил воздух, если наружное давление равно 100 кПа?
Дано:
S = 1дм2 =10-2м2
m = 10кг
р0 = 100кПа
Δl = 20 см =0,2м
А/ -?
Задача 2. Температура воздуха в комнате объемом 70 м3 была 280 К. После того как протопили печь, температура поднялась до 296 К. Найти работу воздуха при расширении, если давление постоянно и равно 100 кПа.
Задачи для самостоятельного решения:
1. Какую работу А совершает газ, количество вещества которого v=2моль, при изобарном повышении температуры на ΔТ=30К?
2. В двух цилиндрах под подвижным поршнем находятся водород и кислород. Сравнить работы, которые совершают эти газы при изобарном нагревании, если их массы, а также начальные и конечные температуры равны.
3. Воздух массой 15 кг нагрели от температуры 100оС до температуры 250оС при постоянном давлении. Чему равна работа при расширении воздуха и изменение его внутренней энергии?
4. Идеальный газ нагрели на 20 К при постоянном давлении, и он совершил работу, равную 249 кДж. Чему равно количество вещества газа, который нагрели?
5. При изобарном нагревании гелия массой 12 г он совершил работу, равную 1 кДж. На сколько изменилась температура газа и какое количество теплоты ему было передано?
Домашнее задание:
Контрольные вопросы:
1. Почему газы при сжатии нагреваются?
2. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображенном на рисунке 2?
Задачи:
1. Азот массой 280 г был нагрет при постоянном давлении на 100 К. Чему равна работа, которую совершил газ при расширении?
2. Газ, изобарно расширяясь при давлении 2×105 Па, совершает работу 200 Дж. Чему равен первоначальный объем газа, если его конечный объем оказался равным 2,5 л?
3. Чему равна работа, которую совершает воздух, изобарно расширяясь при давлении 2×105 Па, когда его нагревают на 17оС? Первоначальный объем воздуха был равен 15 м3, а температура – 0оС.
4. При изобарном нагревании идеального газа его объем увеличился в 3 раза при давлении 3×105 Па. Чему был равен первоначальный объем газа, если для его увеличения потребовалось совершить работу 12,9 кДж?