Изопроцессы в газах
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.
Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.
1. Изобарный процесс. Закон Гей-Люссака.
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческого слова «барос» — вес).
Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.
Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778—1850) и носит название закона Гей-Люссака.
![]() ,
при
Р = const
,
при
Р = const
Из закона Гей-Люссака следует, что при постоянном давлении газа его объем прямо пропорционален температуре.
Для двух состояний газа можно записать выражение
![]()
При увеличении температуры газа в 4 раза, его объем увеличится тоже в 4 раза.

Графически изобарный процесс изображается прямой, которая называется изобарой. Различным давлениям соответствуют разные изобары. Изобара соответствующая более высокому давлению, лежит ниже изобары, соответствующей более низкому давлению.
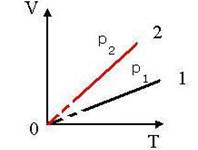
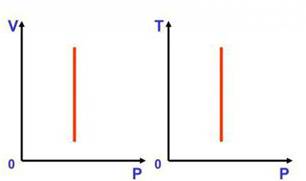
В области низких температур все изобары идеального газа сходятся в точке Т = 0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией.
В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может
Данный закон приближенно можно наблюдать, когда происходит расширение газа при его нагревании в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.
Опыт подтверждения закона:
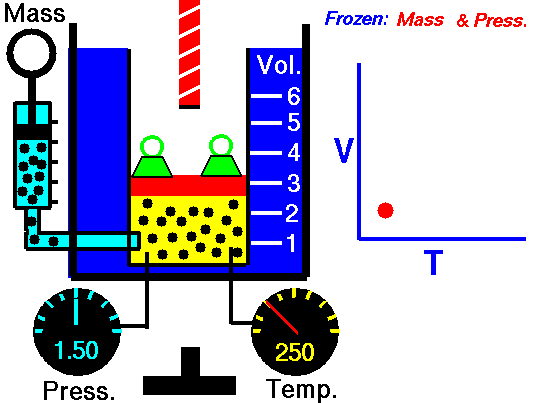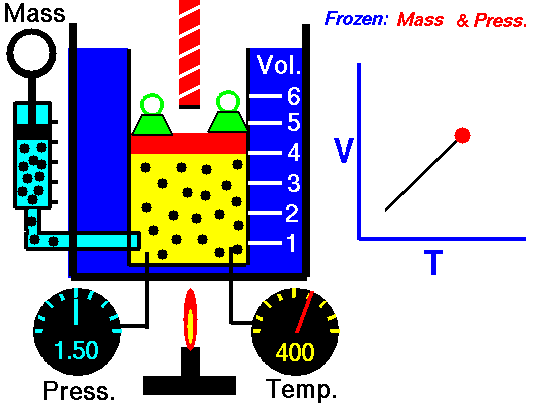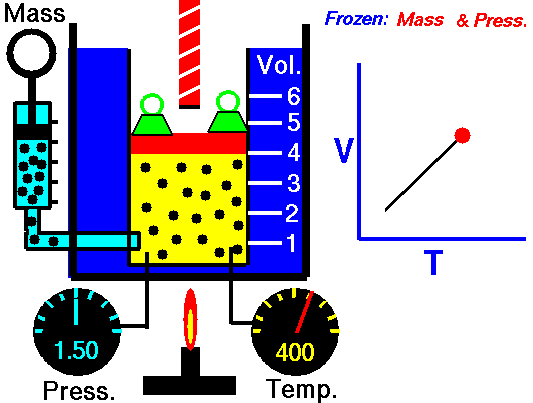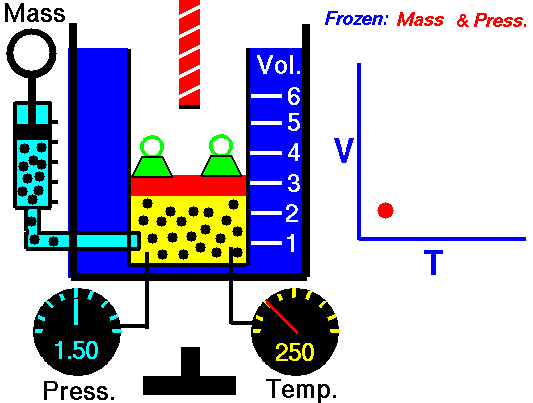
Другим проявлением закона Гей-Люссака в действии является аэростат.
Закон справедлив при температурах, далеких то абсолютного нуля, и малых значениях плотности уравнение может быть использовано для описания свойств любых газов.
2. Изохорный процесс. Закон Шарля.
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (от греческого слова «хорема» — вместимость).
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Этот газовый закон был установлен в 1787 г. французским физиком Ж. Шарлем (1746—1823) и носит название закона Шарля.
![]() ,
при V = const
,
при V = const
Для двух состояний газа можно записать выражение
![]()

Эта зависимость изображается прямой, называемой изохорой. Разным объемам соответствуют разные изохоры.
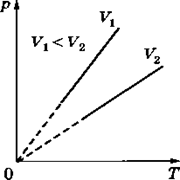
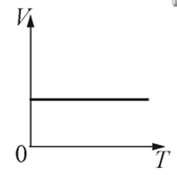
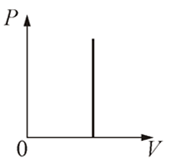
С ростом объема газа при постоянной температуре давление его согласно закону Бойля — Мариотта падает. Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
Все изохоры идеального газа начинаются в точке Т = 0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Данный закон приближенно можно наблюдать, когда происходит увеличение давления газа в любой емкости или в электрической лампочке при нагревании.
Опыт подтверждения закона:
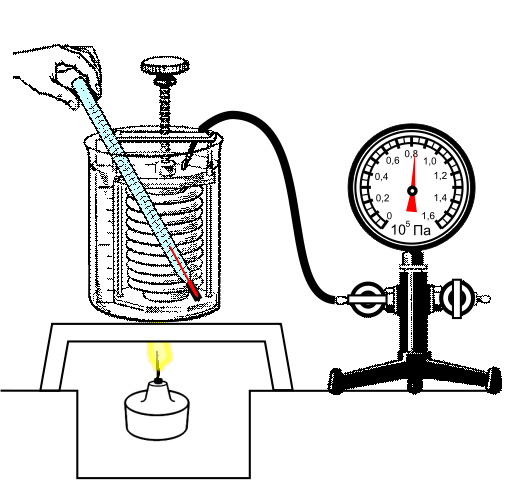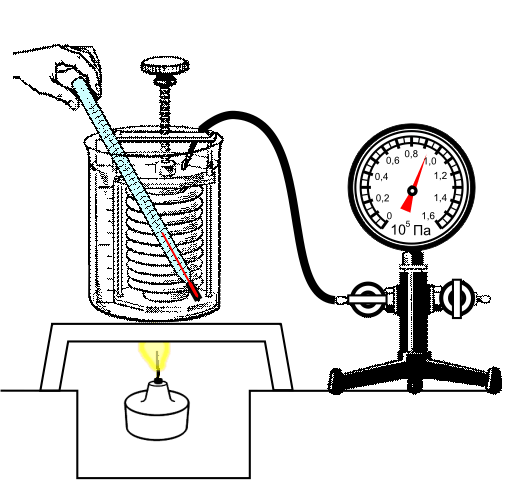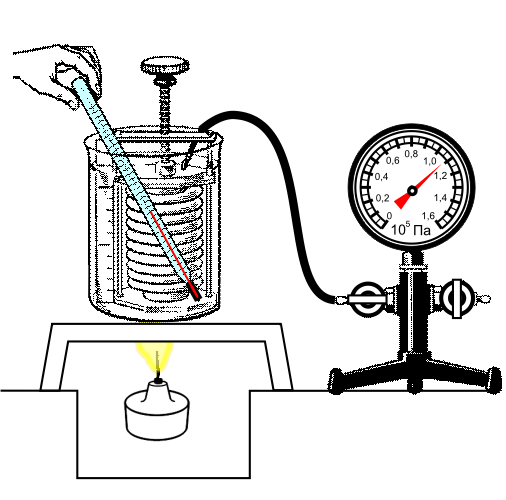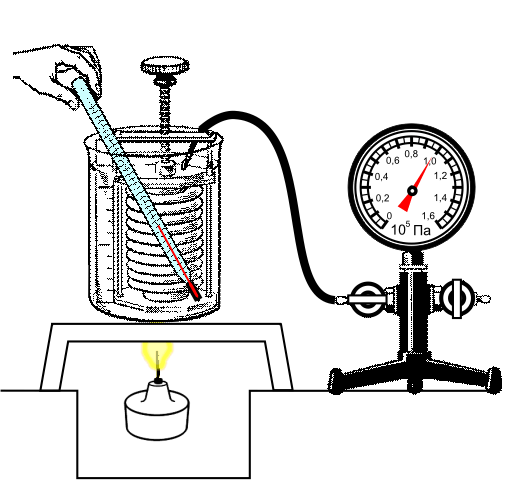
Изохорный процесс используется в газовых термометрах постоянного объема.
Любой баллон, предназначенный для хранения газа, имеет свой запас прочности, максимальное давление, которое он может выдержать. Давление, как описывает закон Шарля, зависит от температуры. Практически можно рассчитать для каждого баллона температуру, до которой этот самый баллон можно нагревать.
Закон Шарля не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
3. Изотермический процесс. Закон Бойля-Мариотта.
Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим.
pV = const при Т = const.
Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Для двух состояний газа можно записать выражение p1 V1 = p2 V2 .
При увеличении объема газа в 2 раза его давление уменьшается тоже в 2 раза.
Закон Бойля-Мариотта открыт в 1662 английским ученым Робертом Бойлем. В 1676 году, независимо от выводов Р. Бойля, закон был описан французским физиком Эдмом Мариоттом, поэтому носит двойное название по фамилиям авторов.
Опыт подтверждения закона:
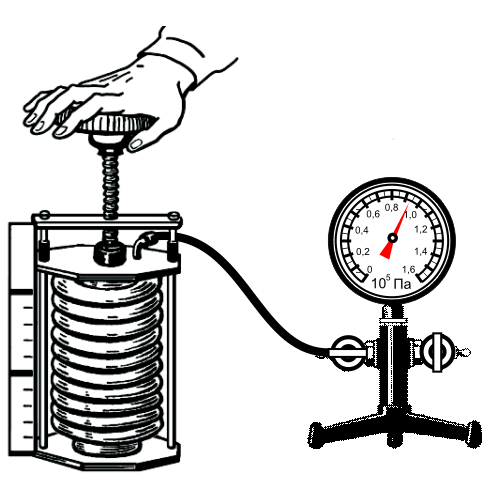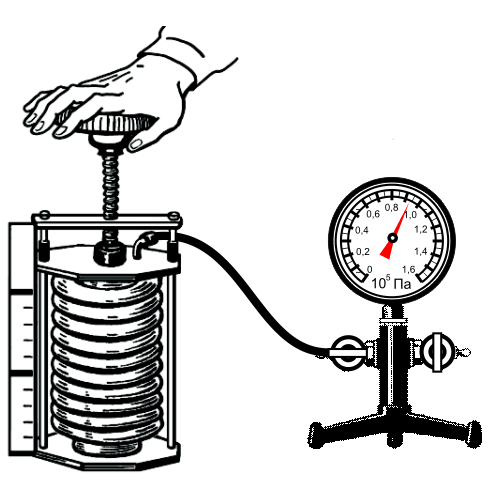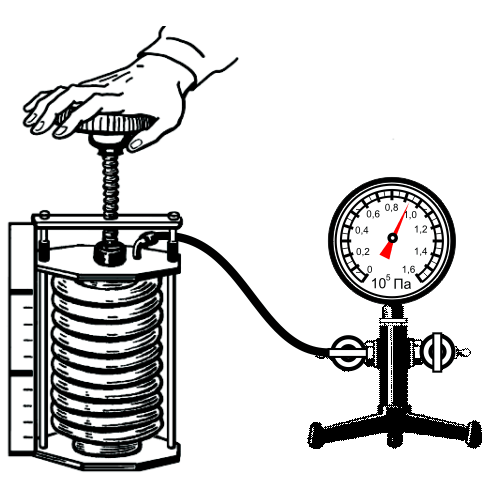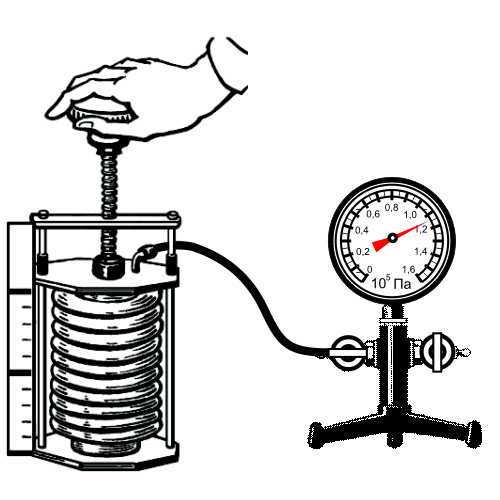
Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой.
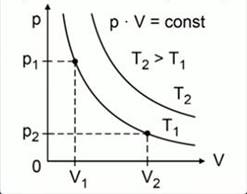
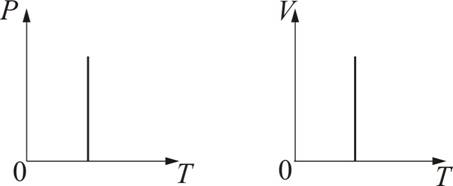
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т2, лежит выше изотермы, соответствующей более низкой температуре Т1.
Закон может быть использован для описания свойств газа в природе или технике при постоянной температуре.
Применение закона: в технике приближенно можно наблюдать в процессе сжатия воздуха компрессором или в результате расширения газа под поршнем насоса при откачке его из сосуда.
Термостаты. В природе закон Бойля Мариотта объясняет, почему пузырьки воздуха, поднимаясь в воде вверх увеличиваются в объеме. На глубине давление жидкости больше, чем на поверхности воды. Одним из аспектов реализации закона в природе является модель работы легких. При дыхании межреберные мышцы и диафрагма периодически изменяют объем грудной клетки. Когда грудная клетка расширяется, давление воздуха в легких падает ниже атмосферного, т.е. «срабатывает» изотермический закон (pV=const), и вследствие образовавшегося перепада давлений происходит вдох. Другими словами воздух идет из окружающей среды в легкие самотеком до тех пор, пока величины давления в легких и в окружающей среде не выровняются. Выдох происходит аналогично: вследствие уменьшения объема легких давление воздуха в них становится больше, чем внешнее атмосферное, и за счет обратного перепада давлений он переходит наружу.
Границы применимости. Закон Бойля-Мариотта справедлив для любых газов, а так же и для их смесей, например, для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Контрольное задание:
1. Составить план обобщенного характера изучения закона
Пункты плана
1. Связь между какими явлениями или величинами выражает данный закон?
2. Формулировка закона.
3. Koгда и кто впервые сформулировал данный закон?
4. Математическое выражение закона.
5. Опыты, подтверждающие справедливость закона.
6. Учёт и использование закона на практике.
7. Границы применения закона.
Примеры решения задач:
Задача 1. Аэростат, наполненный газом при нормальном атмосферном давлении, поднялся в слой воздуха, где давление 500 мм.рт.ст. Во сколько раз увеличится его объем? Изменение температуры не учитывать.
Задача 2. Газ находился в баллоне при температуре 150С и давлении 18 атм. При какой температуре давление газа станет равным 15,5 атм, объем считать неизменным.
Задача 3. Находившийся в закрытом баллоне газ нагрели от 27 до 870С, причем давление возросло на 8 атм. Определить первоначальное значение давление. Расширением баллона пренебречь.
Задачи для самостоятельного решения:
1. Газ занимал объем 12,32л. Его охладили при постоянном давлении на 45 градусов и объем его стал 10,52 л. Какова была первоначальная температура газа?
2. Какой объем займет газ при 77 °С, если при 27 °С его объем был 6 л?
3. При увеличении абсолютной температуры в 1,4 раза объем газа увеличился на 40 см3. Найти первоначальный объем.
4. Температура воздуха в цилиндре 7 °С. На сколько переместится поршень при нагревании воздуха на 20 К, если I = 14 см?
Домашнее задание:
Контрольные вопросы:
1. Вы надули щеки. При этом и объем и давление воздуха у вас во рту увеличиваются. Как это согласовать с законом Бойля — Мариотта?
2. Как можно осуществить изотермический, изобарный и изохорный процессы?
3. Какое состояние системы (газа) считается равновесным?
4. Как качественно объяснить газовые законы на основе молеку- лярно-кинетической теории?
Задачи:
1. При температуре 27 °С давление газа в закрытом сосуде было 75 кПа. Каким будет давление при температуре -13 °С?
2. В нерабочем состоянии при температуре 7 СС давление газа в колбе газополной электрической лампы накаливания равно 80 кПа. Найти температуру газа в горящей лампе, если давление в рабочем режиме возрастает до 100 кПа.
3. При какой температуре находился газ в закрытом сосуде, если при нагревании его на 140 К давление возросло в 1,5 раза?