Уравнение состояния идеального газа

Вывод уравнения Менделеева-Клайперона

Основное уравнение МКТ   , 

учитывая, что кинетическая энергия .

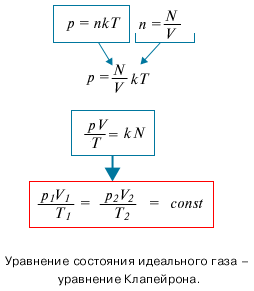
Тогда зависимость давления газа от концентрации молекул и температуры: р = nкТ.

Концентрация молекул ,  число  молекул равно:

Подставим в уравнение р = пкТ выражение для концентрации молекул газа.

Учитывая формулу, концентрацию газа и числа молекул газа можно записать так:

(1) -  Уравнение состояния идеального газа.

где N_a — постоянная Авогадро;

m — масса газа;

µ — его молярная масса.

Произведение постоянной Больцмана к и постоянной Авогадро N_a называют универсальной (молярной) газовой постоянной и обозначают буквой R:

R = kN_A = 1,38 • 10 ^-23 Дж/К • 6,02 • 10²³ 1/моль = 8,31 Дж·моль • К.

Уравнение состояния в форме (1) было впервые получено великим русским ученым Д. И. Менделеевым. Его называют уравнением Менделеева — Клапейрона.

Для чего нужно уравнение состояния? Не только идеальный газ, но и любая реальная система — газ, жидкость, твердое тело — характеризуется своим уравнением состояния. Но только эти уравнения намного сложнее, чем уравнение Менделеева — Клапейрона для идеального (достаточно разреженного) газа.

Практическое применение уравнения Менделеева-Клайперона.

Знать уравнение состояния необходимо при исследовании тепловых явлений. Оно позволяет полностью или частично ответить сразу на три группы различных вопросов.

1. Уравнение состояния позволяет определить одну из величин, характеризующих состояние, например температуру, если известны две другие величины. Это и используют в термометрах.

2. В газовых законах. Зная уравнение состояния, можно сказать, как протекают в системе различные процессы при определенных внешних условиях: например, как будет меняться давление газа, если увеличивать его объем при неизменной температуре, и т. д.

3. В молекулярной физике. Наконец, зная уравнение состояния, можно определить, как меняется состояние системы, если она совершает работу или получает теплоту от окружающих тел.

Уравнение Клайперона

Получим другую форму записи уравнения состояния, называемое уравнением Клапейрона.

Задачи

1. Газ при давлении 8 атм и температуре 12⁰Сзанимает объем 855 л. Каково будет давление, если эта же масса газа при температуре 47⁰ С займет объем 800 л?

2. Газ при давлении 6·10⁵ Па и температуре 20⁰Сзанимает объем 586 л. Найти объем, занимаемый той же массой газа при температуре – 25⁰С и давлении 4·10⁵ Па?

3. Объем газа при давлении 7,2·10⁵ Па и температуре 15⁰С равен 0,6 м³. При какой температуре эта же масса газа займет объем 1,6м³, если давление станет равным 2,25·10⁵ Па?

4. Какова масса воздуха, занимающего объем 150 л при температуре 15⁰С и давлении 1,5·10⁵ Па?

5. В баллоне емкостью 25,6 л находится 1,4 кг азота при давлении 25 атм. Определить температуру газа.

6. При какой температуре 1 см³  газа, содержит 1·10¹⁹ молекул, если давление газа равно 1·10⁴ Па

7. В баллоне емкостью 30 л находится кислород при давлении 72·10⁵ Па и температуре 264 К. Часть газа из баллона выпустили, причем через некоторое время температура газа в баллоне повысилась до 17⁰С, а давление упало до 29·10⁵ Па. Какое количество кислорода выпустили?

8. Газ при давлении 0,2 МПа и температуре 15 °С имеет объем 5 л. Чему равен объем газа этой массы при нормальных условиях?

Домашнее задание:

Контрольные вопросы:

1. Что называют уравнением состояния?

2. Какая форма уравнения состояния содержит больше информации: уравнение Клапейрона или уравнение Менделеева — Клапейрона?

3. Почему газовая постоянная R называется универсальной?

Задачи:

1. Какое количество вещества содержится в газе, если при давлении 200 кПа и температуре 240 К его объем равен 40 л?

2. Каково давление сжатого воздуха, находящегося в баллоне вместимостью 20 л при 12 °С, если масса этого воздуха 2 кг?

3. В баллоне вместимостью 25 л находится смесь газов, состоящая из аргона (Аг) массой 20 г и гелия (Не) массой 2 г при температуре 301 К. Найти давление смеси газов на стенки сосуда.