Модель идеального газа. Основное уравнение МКТ
Качественное объяснение основных свойств вещества на основе молекулярно-кинетической теории не является особенно сложным.
Идеальный газ.
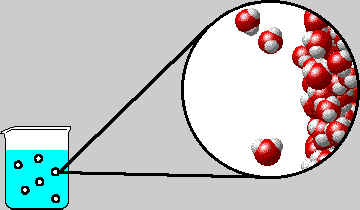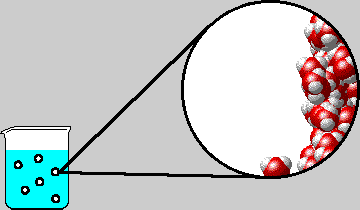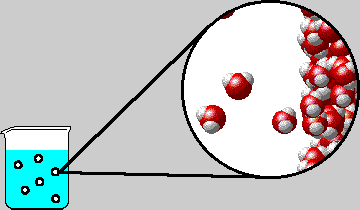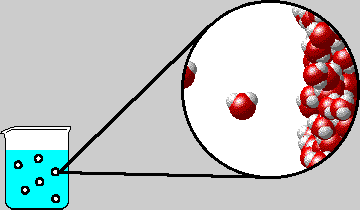
У газа при обычных давлениях расстояние между молекулами во много раз превышает их размеры. В этом случае силы взаимодействия молекул пренебрежимо малы и кинетическая энергия молекул много больше потенциальной энергии взаимодействия. Молекулы газа можно рассматривать как материальные точки или очень маленькие твердые шарики. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать его модель — идеальный газ.
Идеальный газ — это газ, взаимодействие между молекулами которого пренебрежимо мало. Естественно, при столкновении молекул идеального газа на них действует сила отталкивания. Так как молекулы газа мы можем согласно модели считать материальными точками, то размерами молекул мы пренебрегаем, считая, что объем, который они занимают, гораздо меньше объема сосуда.


Давление газа в молекулярно-кинетической теории.
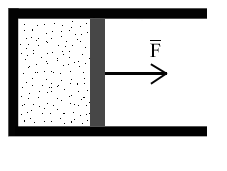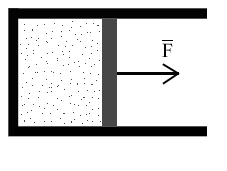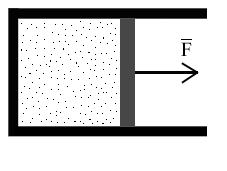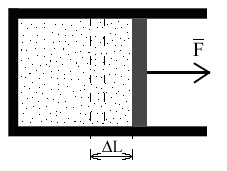
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р0. Как возникает это давление?
Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем.
Идеальный газ — модель реального газа. Согласно этой модели молекулы газа можно рассматривать как материальные точки, взаимодействие которых происходит только при их столкновении. Сталкиваясь со стенкой, молекулы газа оказывают на нее давление.


Вывод основного уравнения МКТ.
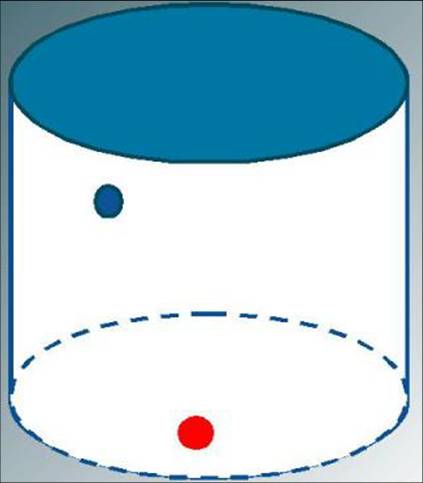
Вычислим давление газа на стенку CD сосуда ABCD площадью S, перпендикулярную координатной оси ОХ (рис.).
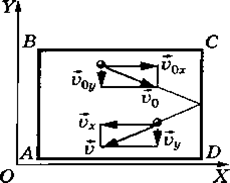
При ударе молекулы о стенку ее импульс изменяется:
∆рх = т0 (vx - v0x).
Так как модуль скорости молекул при ударе не меняется, то ∆рх = 2m0vx.
Согласно второму закону Ньютона изменение импульса молекулы равно импульсу по действовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен 2тп0 | vx |.
Молекул много, и каждая из них передает стенке при столкновении такой же импульс.
За секунду они передадут стенке импульс 2т0vxZ, где Z — число столкновений всех молекул со стенкой за это время.
Число Z, очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число Z пропорционально скорости молекул |vx|. Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой.
Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S:
Z ~ п vx S.
Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с Z ~ п vx S и полный импульс, переданный стенке за 1 с, равен:
Р =2m0 vx Z = m0nv2S.
Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе:
F = m0nv2S.
Учтем, что не все молекулы имеют одно и то же значение квадрата скорости v2. В действительности средняя за секунду сила, действующая на стенку,
пропорциональна не v 2, а среднему квадрату скорости vx:
F = m0nvx 2S.
Так как v х2 =1/3 v2, то
![]()
Таким образом, давление газа на стенку сосуда равно:
![]()
Это и есть основное уравнение молекулярно-кинетической теории газов.
Формула связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.
Связь давления со средней кинетической энергией молекул.
Если через
Е
обозначить среднюю кинетическую энергию поступательного движения молекулы
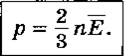
Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии молекул.
Примеры решения задач:
Задача 1. Каково давление газа, если средняя квадратическая скорость его молекул 500 м/с, а его плотность 1,35 кг/м3?
Задача 2. В результате нагревания давление газа в закрытом сосуде увеличилось в 4 раза. Во сколько раз изменилась средняя квадратическая скорость?
Задачи для самостоятельного решения.
1. Найти среднюю кинетическую энергию молекулы одноатомного газа при давлении 20 кПа. Концентрация молекул этого газа при указанном давлении составляет 3 • 10г5 кг3.
2. Во сколько раз изменится давление газа при уменьшении его объема в 3 раза? Средняя скорость движения молекул осталась неизменной.
3. Какова средняя квадратическая скорость движения молекул газа, если, имея массу 6 кг, он занимает объем 5 м3 при давлении 200 кПа?
4. Найти концентрацию молекул кислорода, если давление его 0,2 МПа, а средняя квадратическая скорость молекул равна 700 м/с.
Контрольные вопросы:
1. В баллоне находится газ, количество вещества которого равно 4 моль. Сколько молекул газа находится в баллоне?
2. Как изменится давление идеального газа на стенки сосуда, если в данном объеме скорость каждой молекулы удвоилась, а концентрация молекул не изменилась?
3. Почему молекула при соударении со стенкой действует на нее с силой, пропорциональной скорости, а давление пропорционально квадрату скорости молекулы!
4. Почему и как в основном уравнении молекулярно-кинетической теории появляется множитель?
5. Как средняя кинетическая энергия молекул зависит от концентрации газа и его давления на стенки сосуда?
Домашнее задание:
Задачи:
1. Сравнить давления кислорода и водорода при одинаковых концентрациях молекул и равных средних квадратических скоростях их движения.
2. Вычислить средний квадрат скорости движения молекул газа, если его масса 6 кг, объем 4,9 м3 и давления 200 кПа.