Механические колебания, характеристики. Автоколебания
Понятие механические колебания
Колебательные
процессы встречаются повсюду в природе и технике. В астрономии планеты
периодически обращаются вокруг Солнца, переменные звезды, такие как цефеиды,
периодически меняют свою яркость, движение Луны вызывает приливы и отливы. В
геофизике периодические процессы проявляются при изменении климата, в поведении
океанических течений, в динамике циклонов и антициклонов. Внутри живых
организмов происходят десятки различных периодических процессов с периодом от
доли секунды до года, и т.д.
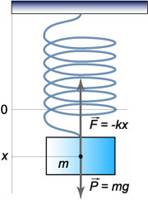
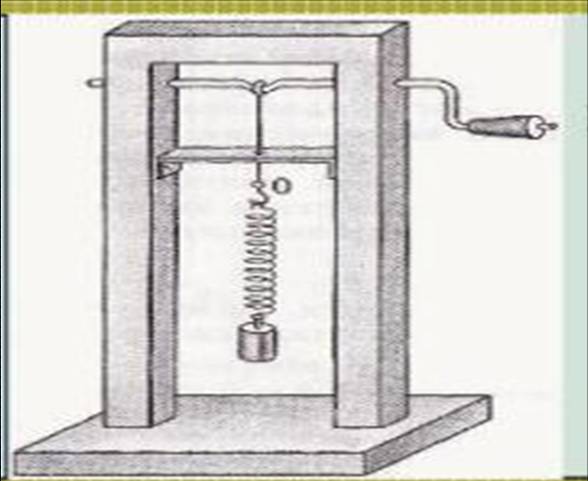
Подвесим пружину к штативу. К нижнему свободному концу подвесим груз массы
m, если груз вывести из положения равновесия, то он начинает совершать
движения вверх-вниз.

Такие движения называются колебательными. Признаком колебательного движения является то, что при колебаниях движения тела повторяются или почти повторяются.
С течением времени колебания постепенно ослабевают, и в конце концов груз остановится.
Механические колебания – это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Свободные и вынужденные колебания. Затухающие колебания
Выделяют свободные и вынужденные колебания.
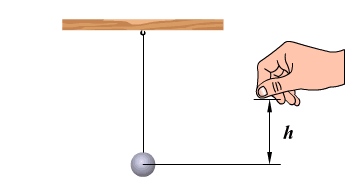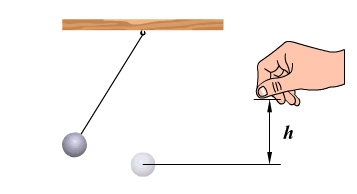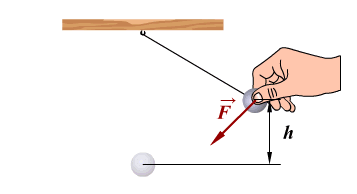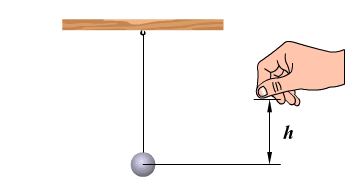
Свободными называются колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия и предоставлена затем самой себе. Груз на пружине или на нити примеры свободных колебаний.
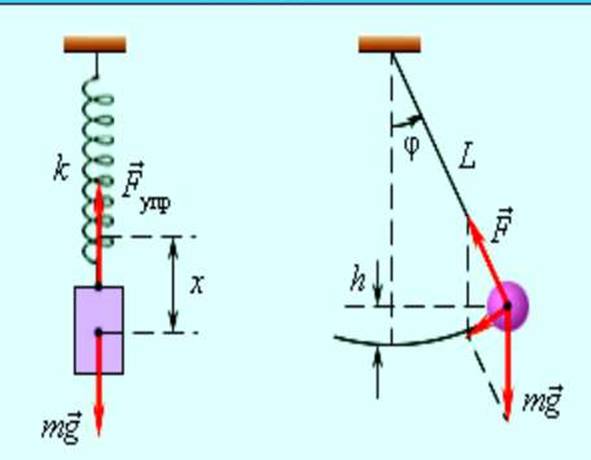
После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил. Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления.
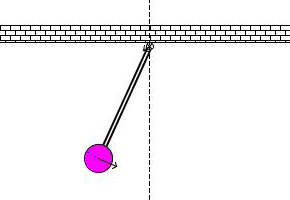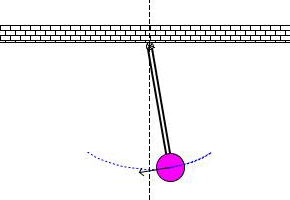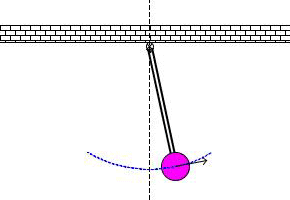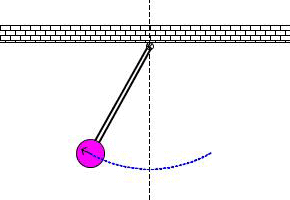
Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.

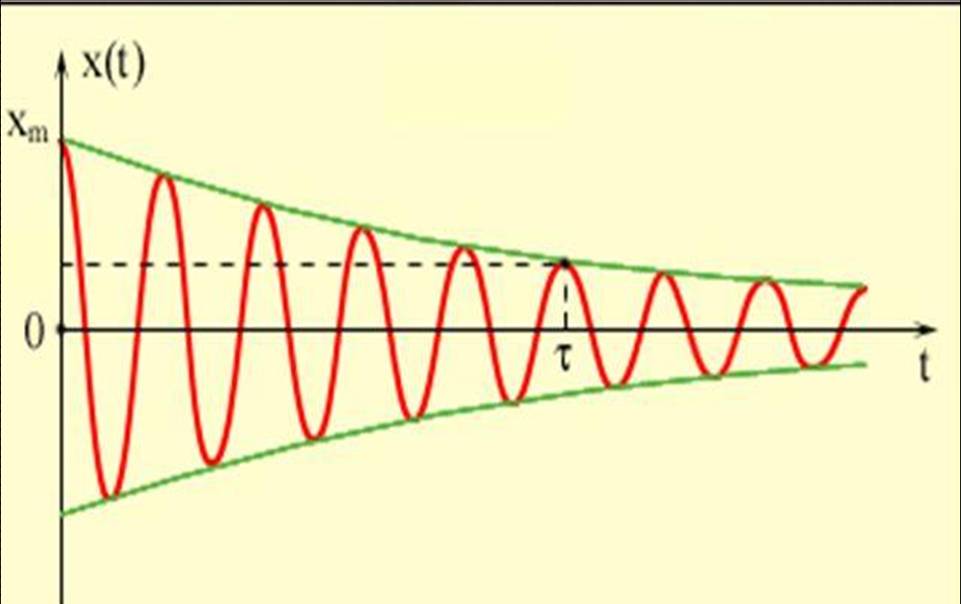
Для того, чтобы колебания не затухали, на тело системы должна действовать периодически изменяющаяся сила.
Вынужденными колебаниями называются колебания под действием внешних периодически изменяющихся сил.
Характеристики колебаний: амплитуда, период, частота колебаний
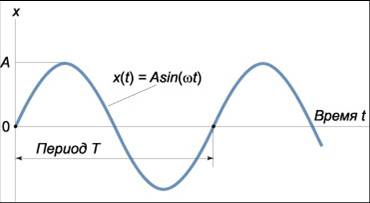
Периодические изменения физической величины в зависимости от времени, происходящие по закону косинуса или синуса, называют гармоническими колебаниями.
Амплитудой гармонических колебаний называют модуль наибольшего смещения тела от положения равновесия.
Уравнение
гармонических колебаний имеет вид:
![]()
В этих формулах A означает амплитуду колебаний,
ωt + φ0 − фазу колебаний,
φ0 − начальную фазу в момент t = 0.
Величина ω называется круговой или циклической частотой колебаний.
Она
связана с периодом колебаний T
соотношением ![]()
Время, за которое тело совершает одно полное колебание называется периодом колебания.
Число колебаний в единицу времени называют частотой колебаний.
ν = 1/Т
Число колебаний за 2πс называется циклической или круговой частотой: ω = 2πν
Математический и пружинный маятник.
Маятником называют, подвешенное на нити или закрепленное на оси тело, которое может совершать колебания под действием силы тяжести.
Груз, подвешенный на пружине называется пружинным маятником.
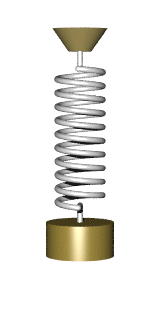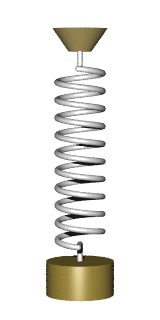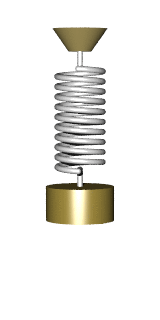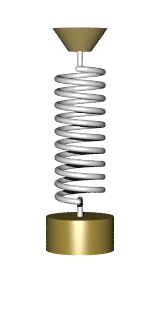
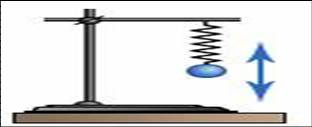
Груз, подвешенный на нити называется математическим маятником.
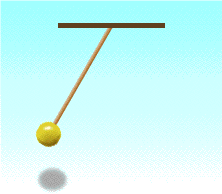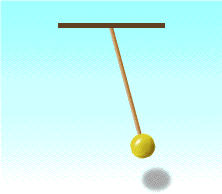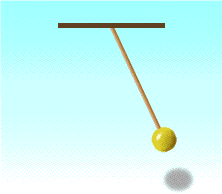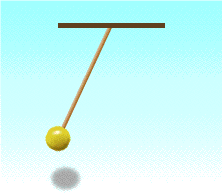
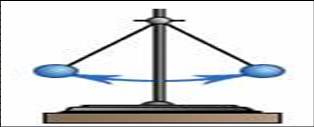
Период математического и пружинного маятника
Если груз на пружине совершает незатухающие гармонические колебания с круговой частотой
![]() ,
то период колебаний пружинного маятника будет равен
,
то период колебаний пружинного маятника будет равен
![]() .
.
Период колебаний математического маятника равен:
![]()
где L −
длина маятника, g − ускорение свободного падения.
Автоколебания. Вынужденные колебания – это незатухающие колебания. Неизбежные потери энергии на трение компенсируются подводом энергии от внешнего источника периодически действующей силы. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах – автоколебаниями.
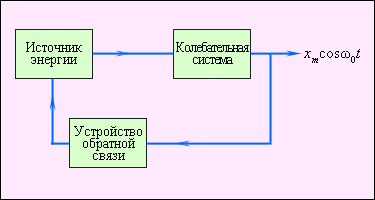
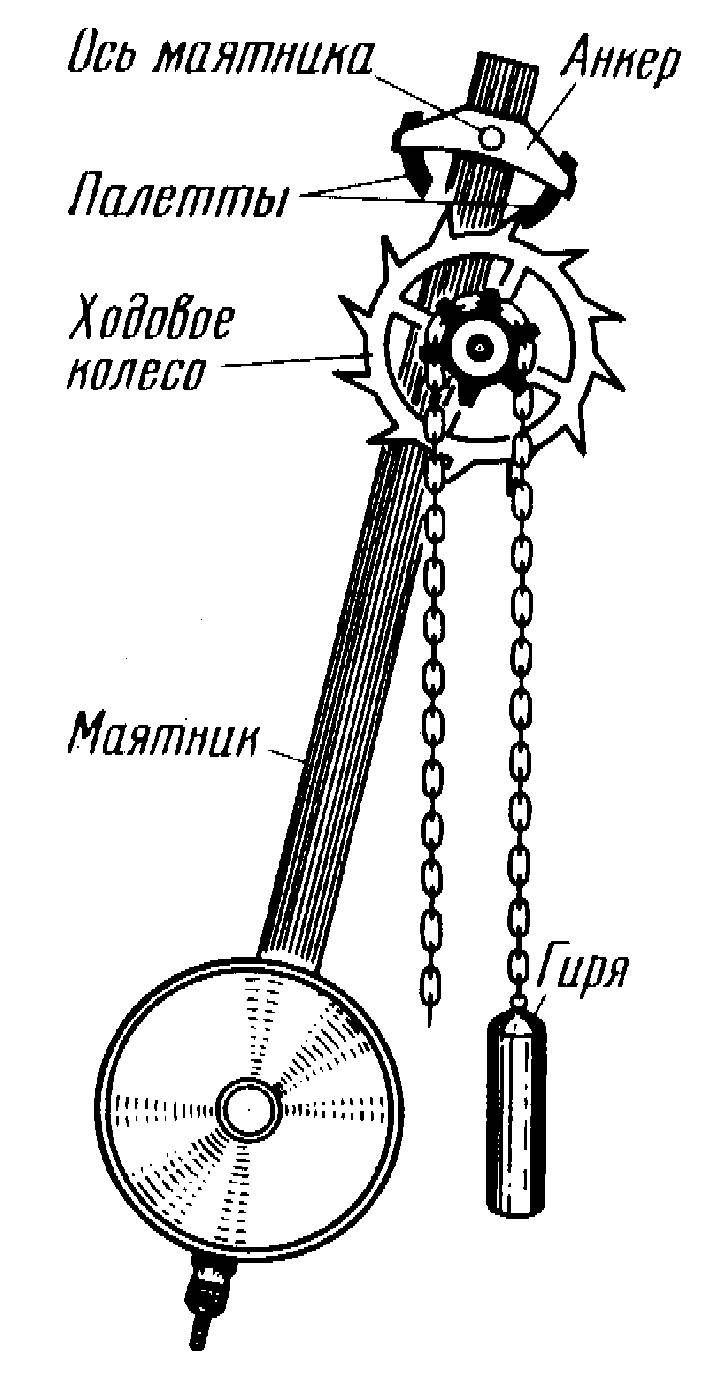
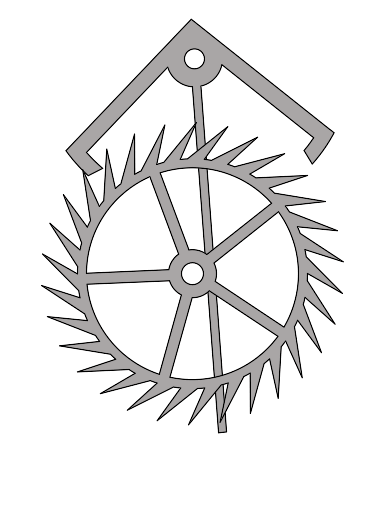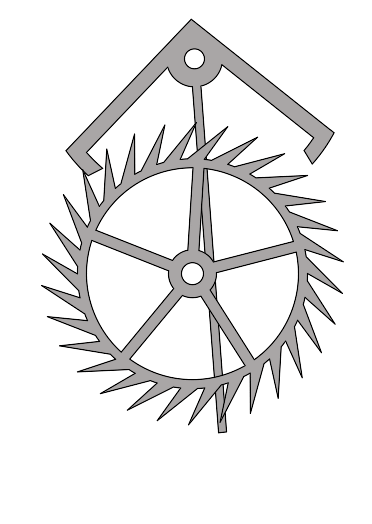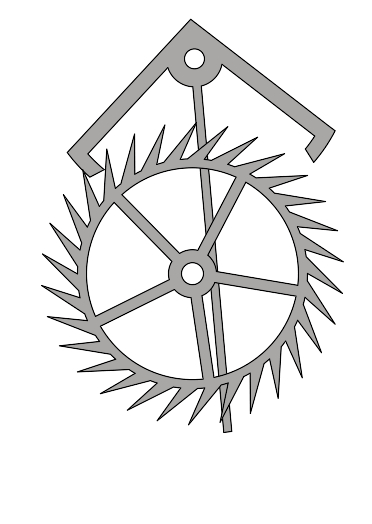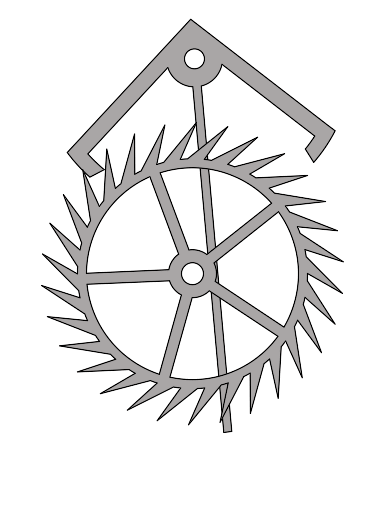
В автоколебательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником. В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов).
Источником энергии может служить энергия деформация пружины или потенциальная энергия груза в поле тяжести. Устройство обратной связи представляет собой некоторый механизм, с помощью которого автоколебательная система регулирует поступление энергии от источника. На рисунке изображена схема взаимодействия различных элементов автоколебательной системы.
Примеры решения задач:
Задача 1.
Материальная точка колеблется с частотой 10 кГц. Определить период и число
колебаний в минуту.
Задача 2. Висящий на пружине груз массой 0,1 кг совершает вертикальные колебания. Определить период гармонических колебаний груза, если для упругого удлинения пружины на 1 см требуется сила0,1 Н. Весом пружины пренебречь.
Задачи для самостоятельного решения
1. Как изменится частота колебаний математического маятника, если его массу увеличить в 4 раза?
2. Математический маятник колеблется с частотой 0,1 кГц. За какое время маятник совершит 10 полных колебаний?
3. Математический маятник длиной 99,5 см за одну минуту совершал 30 полных колебаний. Определить период полного колебания маятника и ускорение свободного падения в том месте, где находится маятник.
Домашнее задание:
Вопросы:
1. Свободные и вынужденные колебания
2. Затухающие колебания
3. Амплитуда, период, частота колебаний
4. Математический, пружинный маятник
5. Период математического, пружинного маятника.
Задачи:
1. Если к некоторому грузу, колеблющемуся на пружине, подвесить гирю массой 100 г, то частота колебаний уменьшится в 1,41 раза. Какой массы груз был первоначально подвешен к пружине?
2. Во сколько раз изменится период колебаний груза, подвешенного на резиновом жгуте, если отрезать 3/4 длины жгута и подвесить на оставшуюся часть тот же груз?
3. Найти период и частоту колебаний математического маятника, длина нити которого равна I. Решить задачу при длине нити, равной: 1) 0,141 м; 2) 1 м; 3) 0,734 м; 4) 2,13 м; 98 м.