
Закон сохранения механической энергии.
Понятие – энергия
Если система тел может совершить работу, то мы говорим, что она обладает энергией.
Энергия характеризует способность тела (или системы тел) совершать работу.

Совершая механическую работу, тело или система тел переходят из одного состояния в другое, в котором их энергия минимальна. Груз опускается, пружина распрямляется, движущееся тело останавливается. При совершении работы энергия постепенно расходуется. Для того чтобы система опять приобрела способность совершать работу, надо изменить ее состояние: увеличить скорости тел, поднять тела вверх или деформировать. Для этого внешние силы должны совершить над системой положительную работу.
Энергия в механике — величина, определяемая состоянием системы — положением тел и их скоростями; изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил.
Кинетическая энергия тела.
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от v1 до v2, то силы совершили определенную работу A.
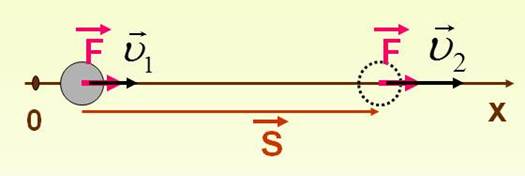
Работа всех приложенных сил равна работе равнодействующей силы.
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы F. В этом случае векторы силы F перемещения S, скорости v и ускорения a направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
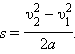 .
.
Отсюда следует, что
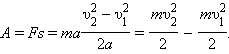 .
.
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
![]()
Теорема о изменении кинетической энергии тела
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
А = Е к2 – Ек1
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью v, равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
![]() .
.
Если тело движется со скоростью v, то для его полной остановки необходимо совершить работу
![]() .
.
Потенциальная энергия тела.
В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.
Работа силы тяжести. Теореме об изменении потенциальной энергии тела.
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести F = mg. Работа этой силы зависит только от вертикального перемещения тела.
Рассмотрим два случая падения тела.
1) Тело вертикально падает вниз
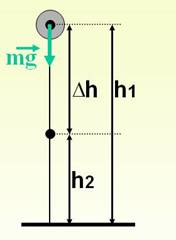
А=FS cosα F = mg Δs = h2 – h1
cosα = 1
А= mg(h1 – h2) = mgh1 – mgh2 = - (mgh2 – mgh1)
2) Тело брошено горизонтально с высоты
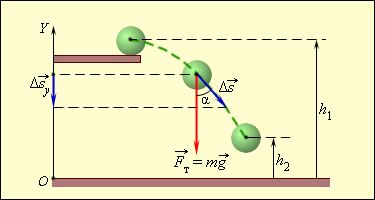
На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения Δs на ось OY, направленную вертикально вверх:
ΔА = Fт Δs cosα = - mgΔsy,
где Fт = Fтy = – mg – проекция силы тяжести,
Δsy – проекция вектора перемещения.
При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY, то сила тяжести совершила работу
А= - mg(h2 – h1) = - (mgh2 – mgh1)
Как и в первом случае получаем, что работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
Eр = mgh.
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
А = - (Е р2 – Ер1)
Потенциальная энергия Eр зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Работа силы упругости. Теорема об изменении потенциальной энергии тела.
Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком:
![]()
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии.
Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
![]() .
.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
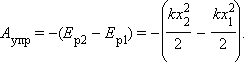 .
.
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Закон сохранения полной механической энергии.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
А = - (Е р2 – Ер1)
По теореме о кинетической энергии эта работа равна изменению кинетической энергии:
А = Ек2 – Ек1
Следовательно
Е к2 – Ек1 = - (Е р2 – Ер1) или Ек1 + Ер1 = Е к2 + Е р2
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
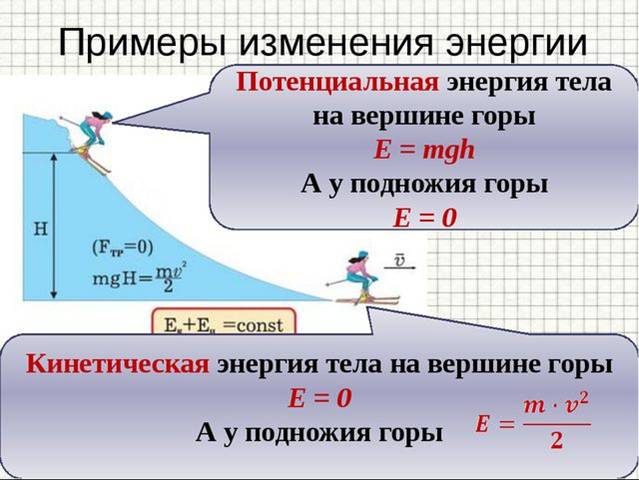
1) Пример сохранения полной энергии при подъеме на гору и спуске
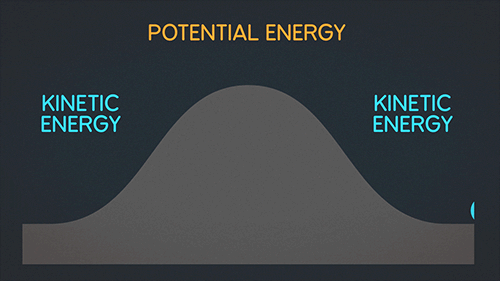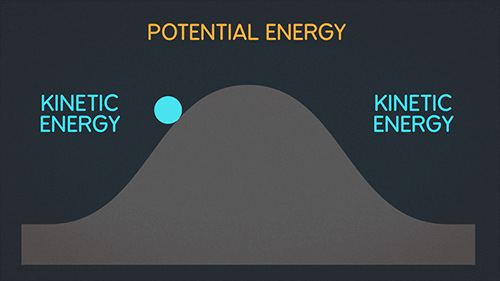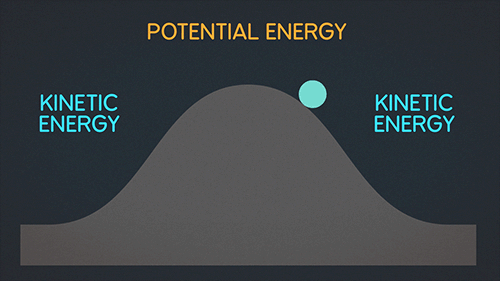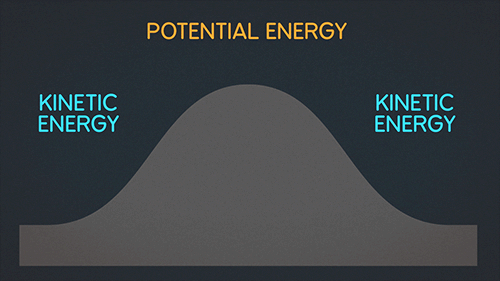
2) Пример сохранения полной энергии тела, подвешенного на нити
Изменение энергии
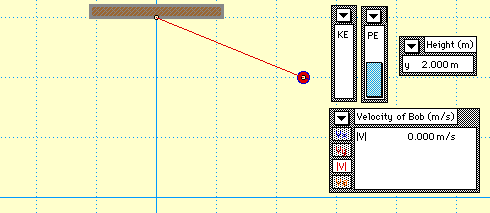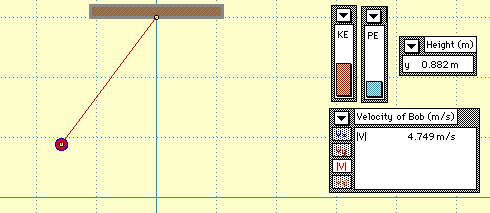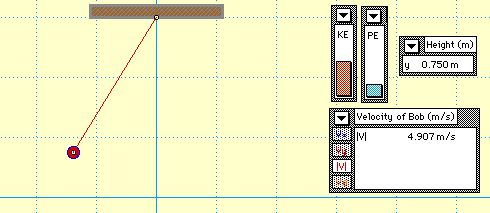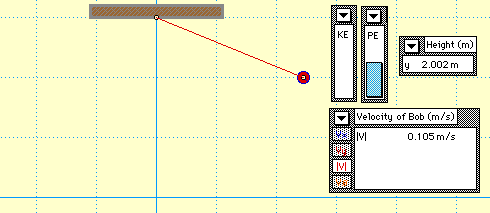
3) Пример сохранении полной энергии при падении и подъеме тела

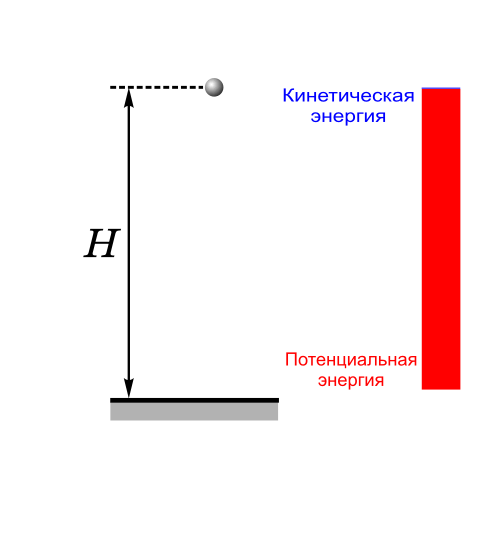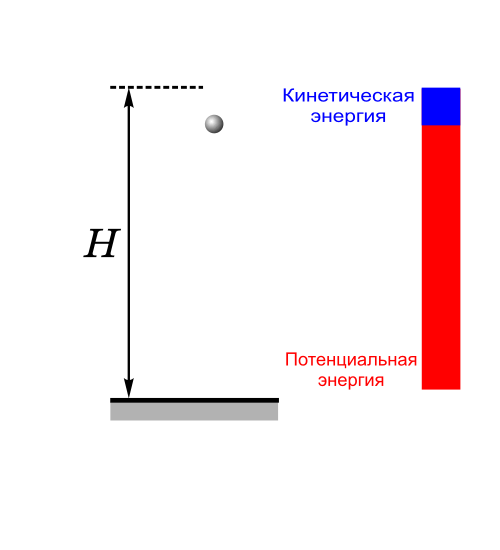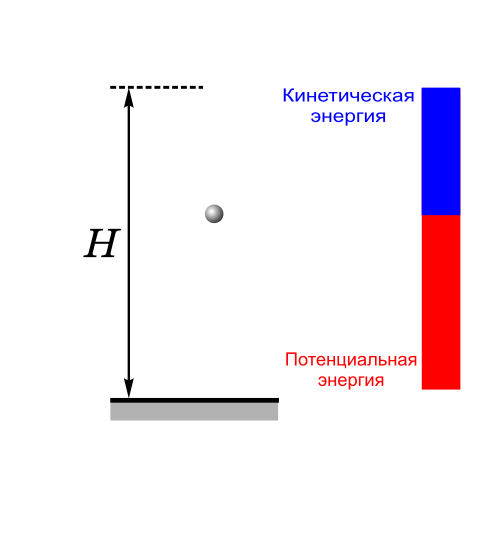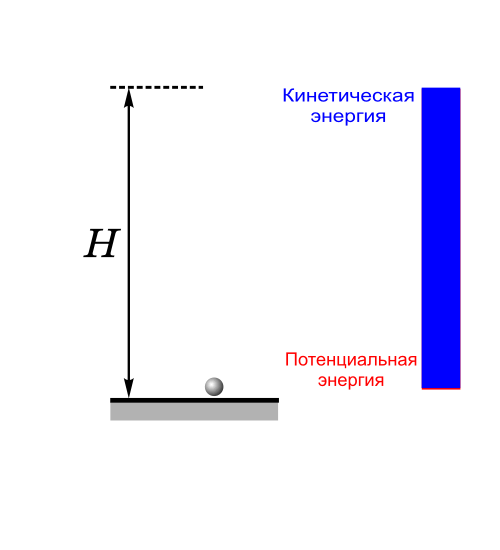
4) Пример сохранения полной механической энергии тела, совершающего колебания на пружине

Контрольное задание
1. Составить план обобщенного характера изучения закона сохранения энергии.
Пункты плана
1. Связь между какими явлениями или величинами выражает данный закон?
2. Формулировка закона.
3. Koгда и кто впервые сформулировал данный закон?
4. Математическое выражение закона.
5. Опыты, подтверждающие справедливость закона.
6. Учёт и использование закона на практике.
7. Границы применения закона.
Примеры решения задач:
Задача 1. Тело массой 400 г свободно падает с высоты 2 м. Найти кинетическую энергию тела в момент удара о землю.
Дано:
m = 0,4кг
h0 = 2м
h = 0м
Екин-?
Решение:
Запишем закон сохранения энергии:
Екин1 + Епот1 = Е кин2 + Е пот2
Так как тело падает свободно, то его скорость равно нулю, следовательно Ек1 = 0.
Поэтому на высоте h0 тело обладает только потенциальной энергией Ер1.
В момент удара о землю тело обладает только кинетической энергией Е к2, так как h = 0м
Поэтому закон сохранения энергии примет вид:
Епот1 = Е кин2
Е кин2 = mgh = 8Дж
Задача 2. Найти потенциальную энергию тела массой 100 г, брошенного вертикально вверх со скоростью 10 м/с, в высшей точке подъема.
Дано:
m = 0,1кг
v0 = 10м/с
Епот-?
Запишем закон сохранения энергии:
Екин1 + Епот1 = Е кин2 + Е пот2
В
момент бросания тело обладает кинетической энергией
На высоте h, тело обладает потенциальной энергией
Потенциальная энергия: Eпот2 = mgh
Поэтому закон сохранения энергии примет вид: Екин1 = Е пот2
Ответ 5 Дж
Задачи для самостоятельного решения
1. Тело массой 10 кг свободно падает с высоты 20м из состояния покоя. 1) Чему равна кинетическая энергия в момент удара о землю? 2) В какой точке траектории кинетическая энергия в 3 раза больше потенциальной?
2. Вагон массой 20т, движущейся со скоростью 2 м/с догоняет вагон массой 40т, движущейся со скоростью 1 м/с, и сцепляется с ним. Насколько изменяется механическая энергия после сцепления?
3. Найти потенциальную и кинетическую энергию тела массой 3 кг, падающего свободно с высоты 5 м, на расстоянии 2 м от поверхности земли.
4. Каковы значения потенциальной и кинетической энергии стрелы массой 50 г, выпущенной из лука со скоростью 30 м/с вертикально вверх, через 2 с после начала движения?
Домашнее задание:
Вопросы:
1. Как выглядит график изменения кинетической энергии тела в зависимости от модуля его скорости? Начертите его.
2. Какую работу совершила сила, действующая на тело, если на¬правление его скорости изменилось на противоположное, а модуль ее остался без изменения?
3. Зависит ли кинетическая энергия тела от выбора системы отсчета?
4. Что называется полной механической энергией системы?
5. Может ли сохраняться механическая энергия системы, на которую действуют внешние силы?
6. Тело падает с высоты Н над поверхностью Земли. Постройте графики зависимости потенциальной, кинетической и полной энергий системы «тело — Земля» от высоты h тела.
Задачи:
1. С какой скоростью двигался поезд массой 1500 т, если под действием тормозящей силы 150 кН он прошел с момента начала торможения до остановки путь 500 м?
2. Бензовоз массой 5 т подходит к подъему длиной 200 м и высотой 4 м со скоростью 15 м/с. В конце подъема скорость уменьшилась до 5 м/с. Коэффициент сопротивления равен 0,09. Найти: а) изменение потенциальной энергии; б) изменение кинетической энергии; в) работу силы сопротивления; г) работу силы тяги; д) силу тяги бензовоза.