Закон всемирного тяготения. Вес и невесомость
Притяжение между телами
Современная физика знает четыре типа сил, или взаимодействий, материальных объектов: гравитационные, электромагнитные, сильные и слабые. Сегодня мы с вами познакомимся с гравитационными силами.
Привычка делает то, что притяжение всех земных предметов Землей кажется нам естественным и обычным явлением. Но когда нам говорят, что предметы притягивают также и друг друга мы не склонны этому верить, т.к. в жизни ничего подобного не замечаем.
Почему закон всемирного тяготения не проявляется постоянно вокруг нас в обычной обстановке? Почему мы не видим, чтобы притягивали друг друга столы, арбузы, люди? (Потому, что для небольших предметов эта сила очень мала.)
Пример: Два
человека, стоящих друг от друга в двух метрах, притягивают один другого, но эта
сила ничтожно мала для людей средней массы – менее 0,01 милиграмм – силы (одна
миллиардная доля той же силы, которая нужна, чтобы сдвинуть нас с места).
Такая сила не может сдвинуть нас с места – этому мешает трение наших подошв о
пол. Удивительно ли, что при обычных условиях мы не замечаем и намека на
взаимное притяжение земных тел? Другое дело, если бы трения не было, тогда ничто
не мешало бы даже слабому притяжению вызвать сближение тел. Притяжение земных
тел можно обнаружить тогда, когда сила трения не служит препятствием.
Груз, подвешенный на
нити, находится под действием силы земного притяжения, и поэтому нить имеет
отвесное направление, но если вблизи груза находится какое – нибудь массивное
тело, которое притягивает к себе груз, то нить слегка отклоняется.
Сила всемирного тяготения.
Ньютон предположил, что ряд явлений, казалось бы не имеющих ничего общего:
- падение тел на Землю,
- обращение планет вокруг Солнца,
- движение Луны вокруг Земли,
- приливы и отливы
вызваны одной причиной.
Проведя многочисленные расчеты, Ньютон пришел к выводу, что все тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Ньютон был первым, кто строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила тяготения, действующая между любыми телами Вселенной.
Вот ход рассуждений, приведенных в главном его труде «Математические начала натуральной философии»: «Брошенный на Землю камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше».

Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определенной скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался бы вокруг нее подобно тому, как планеты описывают в небесном пространстве свои орбиты.
Сейчас нам стало настолько привычным движение спутников вокруг Земли, что разъяснять мысль Ньютона подробнее нет необходимости.
Итак, по мнению Ньютона, движение Луны вокруг Земли или движение планет вокруг Солнца — это тоже свободное падение, которое длится, не прекращаясь, миллиарды лет. Причиной такого падения (идет ли речь действительно о падении обычного камня на Землю или о движении планет по их орбитам) служит сила тяготения.


Как и всем другим телам, Земля должна сообщать Луне ускорение, не зависящее от массы Луны.
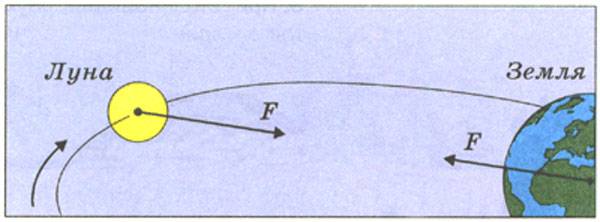
Роль масс притягивающихся тел
Ускорение свободного падения имеет ту любопытную особенность, что оно одинаково для всех тел, для тел любой массы. А ведь ускорение по второму закону Ньютона а = F/m.
Как же объяснить, что ускорение, сообщаемое телу силой притяжения Земли, одинаково для всех тел?
Единственное
объяснение, которое можно найти этому, состоит в том, что сама сила притяжения
пропорциональна массе притягиваемого тела. Действительно, в этом случае
увеличение массы тела, даже вдвое. Приведет к увеличению и силы вдвое. Ускорение останется прежним. Ньютон сделал этот единственный возможный
вывод:
сила всемирного тяготения пропорциональна массе того тела, к которому она
приложена. Но ведь тела притягиваются взаимно (третий закон Ньютона).
Следовательно, не только Земля притягивает тело, но и тело притягивает
Землю и эта сила притяжения пропорциональна уже массе Земли. А силы эти
одинаковые. Отсюда следует, что сила взаимного притяжения пропорциональна массам
обоих тел. Это значит: что сила пропорциональна
произведению масс обоих тел.
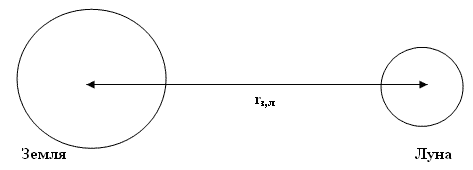
Роль расстояния между телами
Ньютон считал, что отсчитывать надо расстояние не от поверхности, а от центра Земли. Радиус Земли – 6400 км. Понятно, что несколько десятков, сотен или даже тысяч метров над поверхностью Земли не могут заметно изменить значение ускорения свободного падения.
Чтобы выяснить, как влияет расстояние между телами на силу их взаимного притяжения, нужно было бы узнать, каково ускорение тел, удалённых от Земли на достаточно большие расстояния. Ньютон рассчитал отношение радиуса орбиты Луны к радиусу Земли. Отношение равнялось – 60. А отношение ускорения свободного падения на Земле к центростремительному ускорению, с которым обращается вокруг Земли Луна, равнялось – 3600. Следовательно, ускорение обратно пропорционально квадрату расстояния между телами.
Но по второму закону Ньютона сила и ускорение связаны прямой зависимостью, следовательно, сила обратно пропорциональна квадрату расстояния между телами.
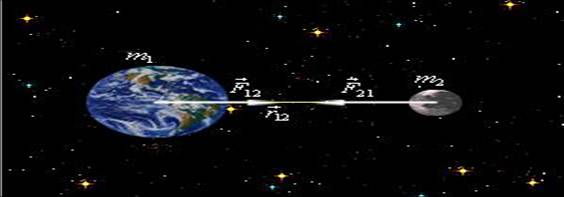
2) По третьему закону Ньютона F1.2 = F2.1
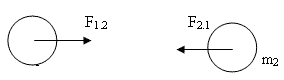
Если
F1.2
~
m1.
F2.1
~
m2
, Следовательно F ~ m1. m2
3)
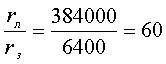
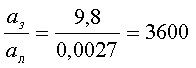
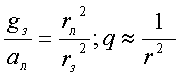
Но F = mg, следовательно
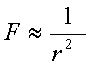
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
![]()
Коэффициент пропорциональности G называется гравитационной постоянной.
Границы применимости закона:
1) только для материальных точек,
2) для тел, размеры которых значительно меньше, чем расстояния между ними,
3) для тел имеющих форму шара,
4) для шара большого радиуса, взаимодействующего с телами, размеры которых
значительно меньше размеров шара.
Пример решения задач
На каком расстоянии от поверхности Земли сила притяжения космического корабля к ней станет в 100 раз меньше, чем на поверхности Земли?Задачи
Задачи для самостоятельного решения:
1. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
2. Оценить порядок значения силы взаимного тяготения двух кораблей, удаленных друг от друга на 100 м, если масса каждого из них 10 000 т.
3. Во сколько раз уменьшится сила притяжения к Земле космического корабля при его удалении от поверхности Земли на расстояние, равное радиусу Земли? пяти радиусам Земли?
4. Среднее расстояние между центрами Земли и Луны равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке отрезка, соединяющего центры Земли и Луны, тело будет притягиваться ими с одинаковой силой?
5. Два тела одинаковой массы, находящиеся на некотором расстоянии друг от друга, притягиваются с силой F. Какой станет сила притяжения F, если, не изменяя расстояния между телами, половину массы первого тела перенести на второе?
Контрольное задание
Составить план обобщенного характера изучения закона.
1. Связь между какими явлениями или величинами выражает данный закон?
2. Формулировка закона.
3. Koгда и кто впервые сформулировал данный закон?
4. Математическое выражение закона.
5. Опыты, подтверждающие справедливость закона.
6. Учёт и использование закона на практике.
7. Границы применения закона.
Домашнее задание:
Задачи:
1. Каково ускорение свободного падения на высоте, равной половине радиуса Земли?
2 . Средний радиус планеты Меркурий 2420 км, а ускорение свободного падения 3,72 м/с2. Найти массу Меркурия.