Практическое занятие № 2 «Определение расстояния до звезд, параметры звезд»
Теория
1. Определение расстояний до звезд.
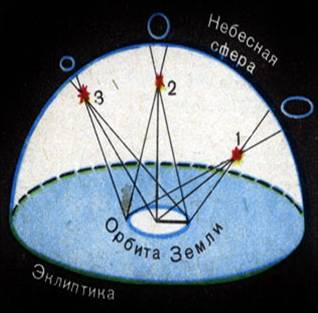
Годичным параллаксом звезды ρ называют угол, под которым со звезды можно было бы видеть большую полуось земной орбиты (равную 1 а. е.), если она перпендикулярна лучу зрения.
Годичные параллаксы звезд
Чем больше расстояние D до звезды, тем меньше ее параллакс. Параллактическое смещение положения звезды на небе в течение года происходит по маленькому эллипсу или кругу, если звезда находится в полюсе эклиптики.
Расстояние до звезды
,
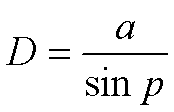где а - большая полуось земной орбиты.
При малых углах
,
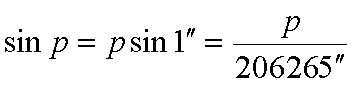если р выражено в секундах дуги.
Тогда, приняв а = 1 а. е., получим:
.
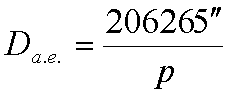Расстояние, которое свет проходит в течение года, называется световым годом. Эта единица используется для измерения расстояния наряду с парсеком (пк).
Парсек - расстояние, с которого большая полуось земной орбиты, перпендикулярная лучу зрения, видна под углом в 1".
Расстояние в парсеках равно обратной величине годичного параллакса, выраженного в секундах дуги. Например, расстояние до звезды α Центавра равно 0,75" (3/4"), или 4/3 пк. Dпк=1/р"
1 парсек = 3,26 светового года = 206 265 а. е. = 3*1013 км.
2. Цвет, спектры и температура звезд
Шкала звездных величин введена таким образом, что чем меньше число, которым выражается звездная величина, тем звезда ярче.
Красный (класс M) - 2000-3500 градусов.
Оранжевый (класс K) - от 3500 до 5000 градусов.
Жёлтый (класс G) - 5-6 тысяч градусов. К данному типу относится и наше Солнце.
Жёлто-белый (класс F) - от 6000 К до 7500 К.
Белый (класс A) - 7500 К - 10000 К.
Бело-голубой (класс B) - 10-30 тысяч градусов.
Голубой (класс O) - 30-60 тысяч К.
3. Массы и размеры звезд
Сумма масс двойных звезд, составляющих пару, в массах Солнца:
,
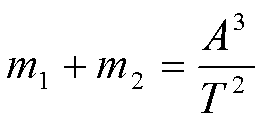где m1 и m2 – массы двух звезд, имеющих период Т.
А – большая полуось орбиты звезды, обращающейся вокруг другой звезды.
Чтобы определить массу каждой звезды, надо изучить движение компонентов относительно окружающих звезд и вычислить их расстояния А1 и А2 от общего центра масс. Тогда получим второе уравнение
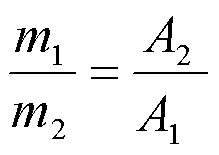. Из
системы двух уравнений найдем обе массы отдельно.
Если известно расстояние D до двойной звезды в парсеках и большая полуось орбиты звезды-спутника в секундах дуги, равная а", то в астрономических единицах она будет равна: Аа.е.= а" * D,
или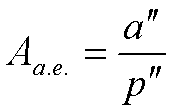 
.
4. Размеры звезд.
Относительный линейный диаметр звезд, имеющих известную температуру Т, находят из формулы
,
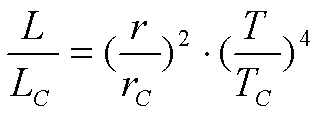где r - радиус звезды,
L-светимость,
rС, TС относятся к Солнцу,
LС= l.
Отсюда радиус Звезды находим по формуле в радиусах Солнца:
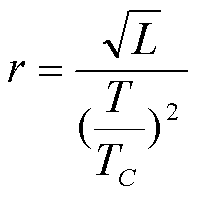
5. Видимая и абсолютная звездная величина
Абсолютную звездную величину М по известной видимой звездной величине m при реальном расстоянии до звезды D можно найти по формуле:
М=m+5-5lgD или М=m+5-5lgp,
где р выражено в секундах дуги.
Для Солнца Мс≈5.
Зная абсолютную звездную величину М какой-нибудь звезды, легко вычислить ее светимость L. Принимая светимость Солнца LС=1, по определению светимости можно записать, что
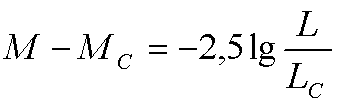
L=2,5125-М или Lg L=0,4 (5-М)
Отношение видимой яркость двух любых звезд связано с разностью их видимых звездных величин соотношением:
I1/I2=2,512m2-m1, или Lg L1/L2=0,4 (m2 - m1)
Виды заданий:
1. Определение расстояния до звезды (1 балл)
2. Определение абсолютной звездной величины и светимости по известной видимой звездной величине и расстоянию до звезды. (1 балл)
3. Определение размеры звезд (1 балл)
4. Определение масс звезд в двойных системах (1 балл)
5. Классы звезд (1 балл)
Критерии оценок:
Оценка соответствует сумме набранных обучающимся баллов:
5 баллов - 5 (отлично)
4 балла – 4 (хорошо)
3 балла – 3 (удовлетворительно)\
2,1 балл 2 (неудовлетворительно)
Тренировочные задачи:
1. Годичный параллакс звезды Бетельгейзе 0,005". Определите расстояние до звёзды (в парсеках и световых годах).
Дано: Решение:
р = 0,005". Dпк=1/P"
D-? D = 200 пк = 720св.лет
2. Зная видимую звёздную величину (m=0,08) звёзды Капелла, расстояние до нее в парсеках 12,9, определите ее абсолютную звёздную величину (M) и светимость (L)Дано: Решение:
m=0,92 Абсолютная звездная величина: M=m+5-5 lg12,9 = 0,08+5-5*1,11 =-0,47
D= 132,9пк Сравнивая ее с абсолютной звездной величиной Солнца МС=4,8,
M-? найдем светимость звезды, выраженную в светимостях Солнца:
L-?
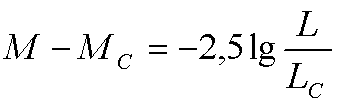или
откуда L/LC
=102,1=125.
3. Найти размеры звезды Бетельгейзе в радиусах Солнца, если температура ее поверхности 3500 Кельвина, а светимость в 140000 раз больше, чем у Солнца. ТC=600К.
Дано: Решение:
Т=3500К
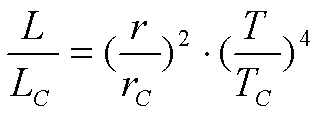
LC=1 r=641 радиусов Солнца
L/LC=140000
r-?
4. Период обращения двойной звезды 100 лет. Большая полуось видимой орбиты 2", параллакс звезды 0,05". Звезды отстоят от центра масс на расстоянии, относящихся как 2:1. Определит сумму масс и массу каждой звезды.
Дано: Решение:
р= 0,05"
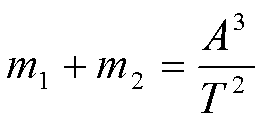А=а"/р"=40а.е
m1 + m2 = 64000/10000=6,4 масс Солнца
Т = 100 лет
а = 2", m2 = 2m1 m1 + 2m1 =40 3 m1=40 m1=13,3 масс Солнца m2=26,6 масс Солнца
m1 + m2 -?
5. Во сколько раз звезда 3,4 звездной величины слабее, чем Сириус, имеющий видимую звездную величину -1,6? Чему равны абсолютные величины этих звезд, если расстояние до обеих составляет 3 пк? Решение
Дано: Решение:
m1=3,4 I1/I2=2,512m2-m1, I1/I2=2,512-1,6–3,4= 100раз
m2= -1,6
I1/I2-? M=m+5-5 lg 3 = 3,4+5-5*0,5=6
М-?
m1 + m2-? М=m+5-5 lg 3 = -1,6+5-5*0,5=1
Дополнительные задачи:
1. Во сколько раз Сириус (m= -1,6) ярче, чем Альдебаран (m=1,06)? Солнце (m= -26) ярче, чем Сириус?
2. Во сколько раз меняется блеск Марса, если его видимая звездная величина колеблется от +2,0m до -2,6 m?
3. Одна звезда ярче другой в 16 раз. Чему равна разность их звездных величин?
4. Звездная величина звезды Вега около + 0,03m , звезды Альтаир + 0,75m , а звезды Денеб + 1, 25m . Какая из этих звезд выглядит ярче и почему? Укажите, каким созвездиям принадлежат данные звезды.