Небесная механика. Законы Кеплера, открытие планет

Иоганн Кеплер (1571-1630). Выдающийся немецкий астроном и математик, открывший законы движения планет вокруг Солнца. Кеплер был активным сторонником учения Коперника и своими работами способствовал его утверждению и развитию.

В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.

1. Законы Кеплера

1) Первый закон Кеплера. 

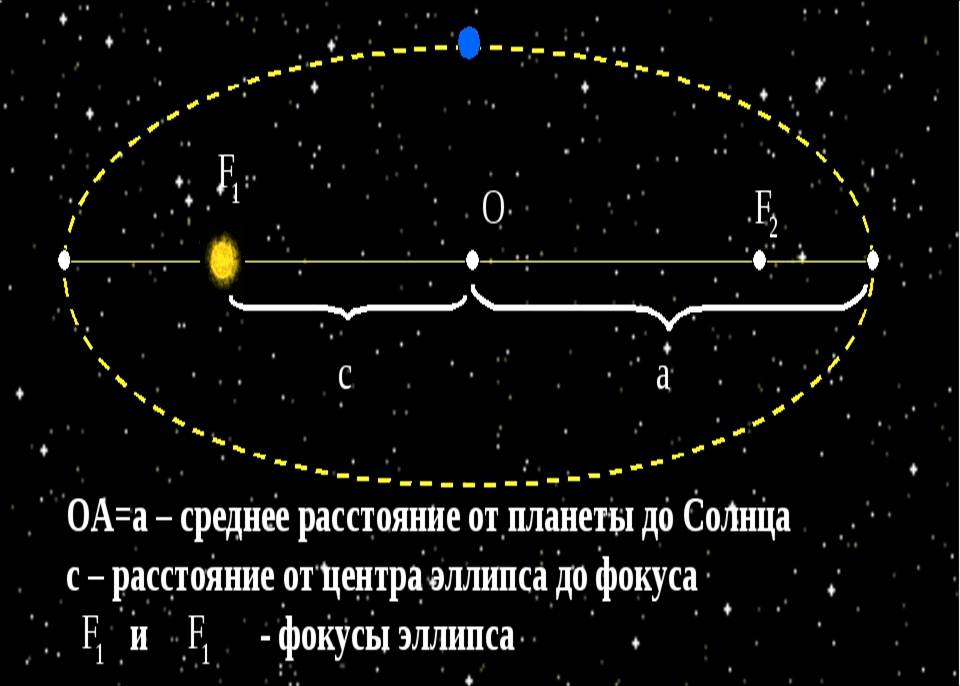
Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце.

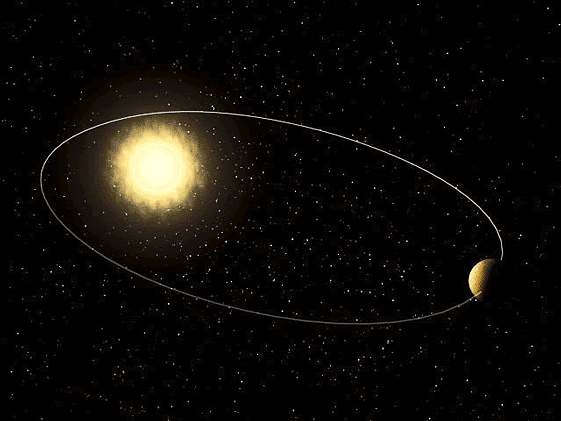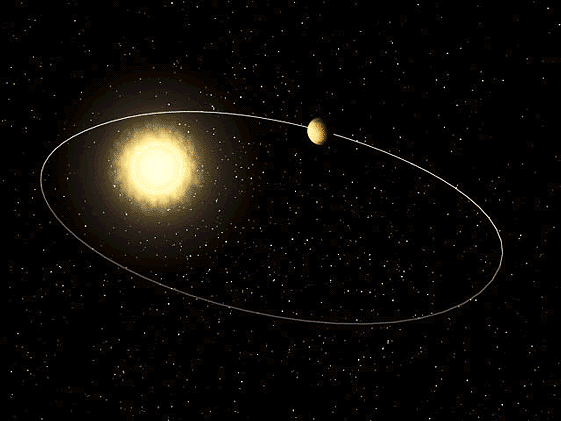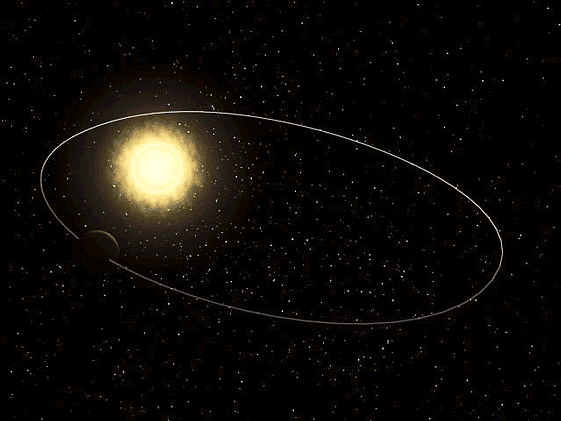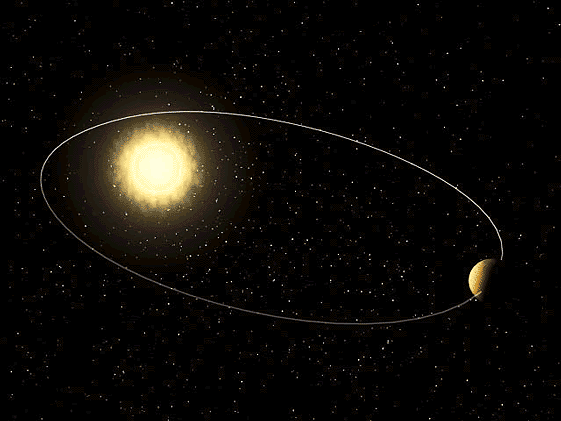
Первый закон Кеплера (http://2012god.ru/spasibo-kepleru/)

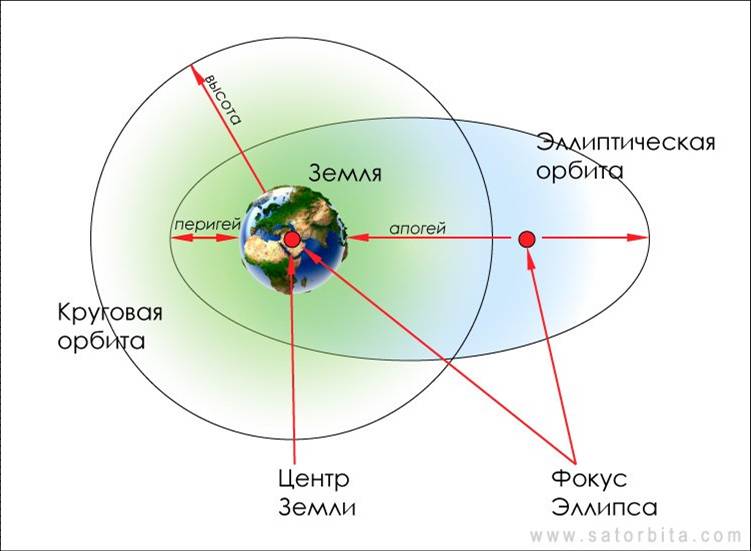
Эллипсом называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной.

Эта сумма расстояний равна длине большой оси DA эллипса.

Точка О - центр эллипса, К и S - фокусы.

Солнце находится в данном случае в фокусе S.

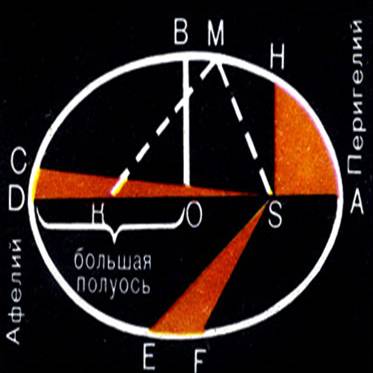
DO = OA = a - большая полуось эллипса.

Большая полуось является средним расстоянием планеты от Солнца:

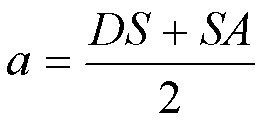
Ближайшая к Солнцу точка орбиты А называется перигелием, а самая далекая от него точка D - афелием.

Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет равен отношению расстояния фокуса от центра (OK=OS) к длине большой полуоси а, т. е. .

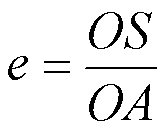При совпадении фокусов с центром (е=0) эллипс превращается в окружность.

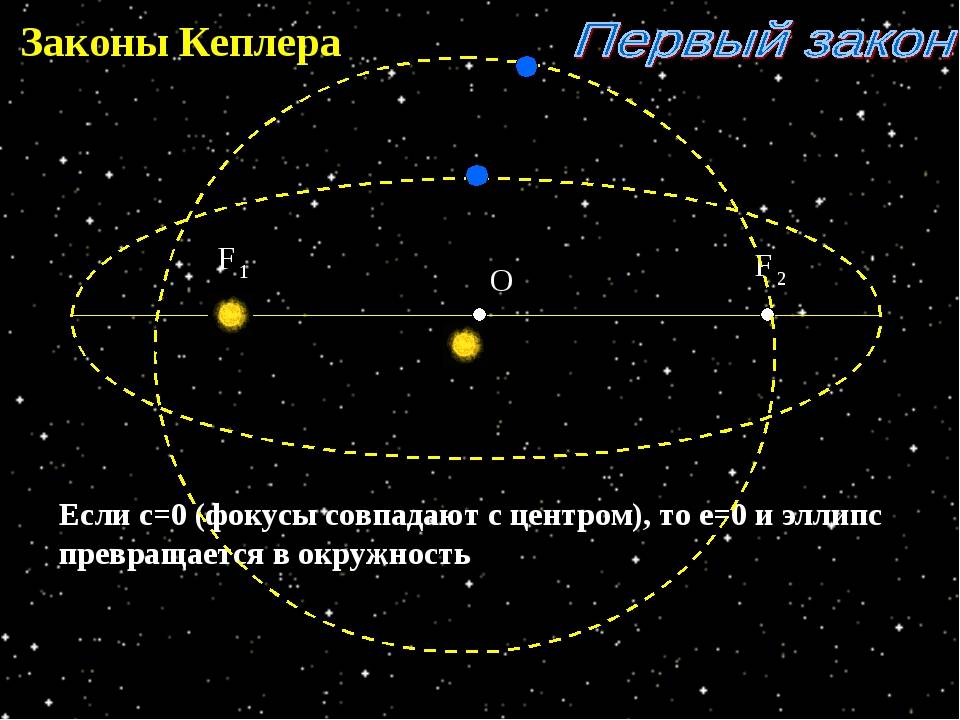
Орбиты планет - эллипсы, мало отличающиеся от окружностей; их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е=0,017.

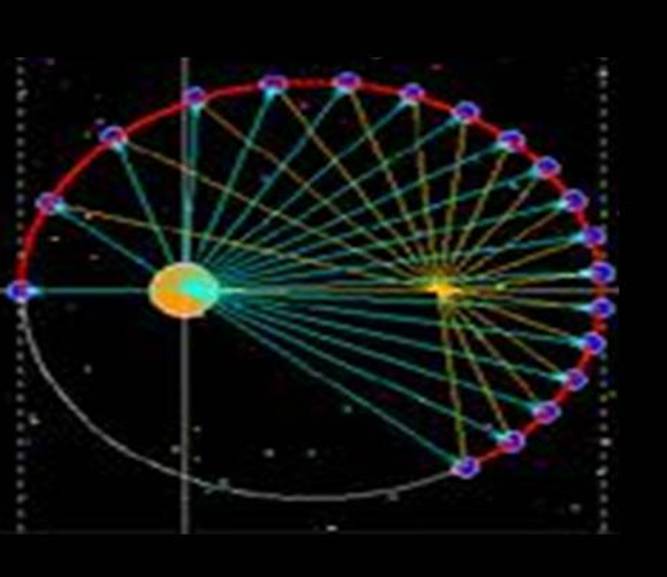
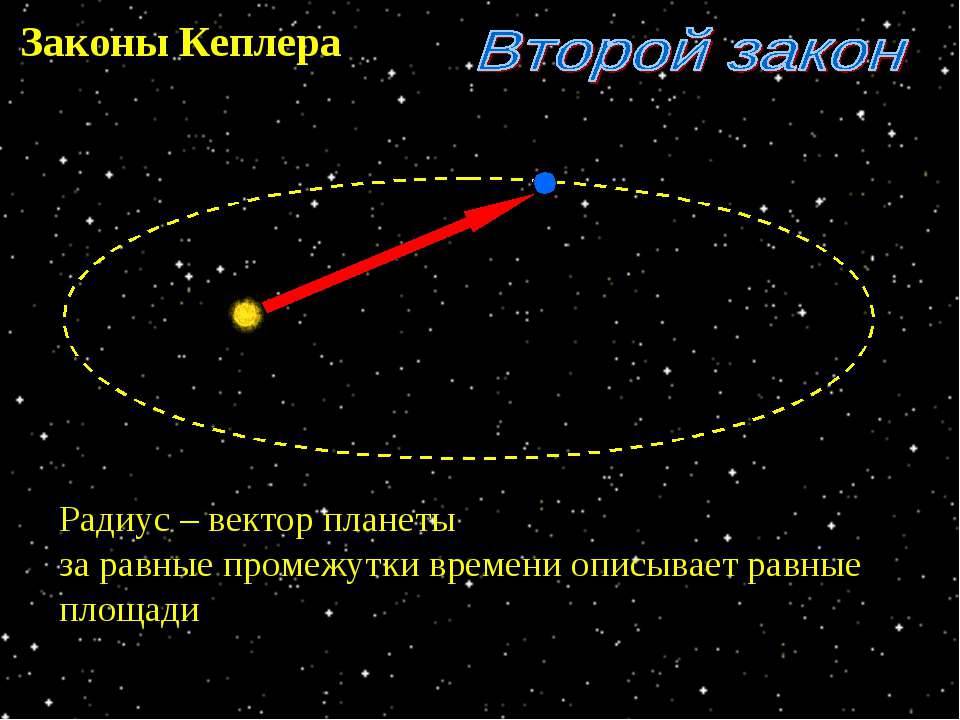
2) Второй закон Кеплера (закон площадей). 

Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади, т. е. площади SAH и SCD равны, если дуги и описаны планетой за одинаковые промежутки времени. Но длины этих дуг, ограничивающих равные площади, различны: >  .

 .

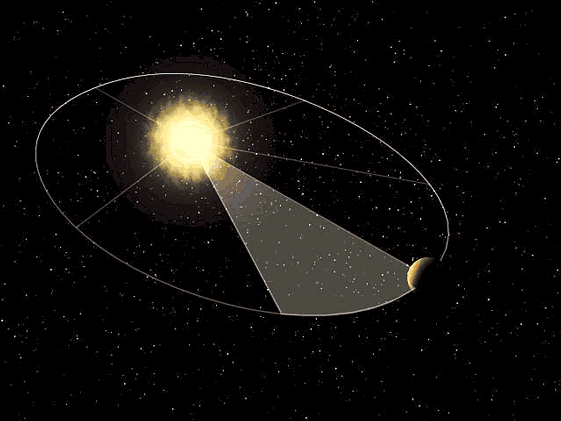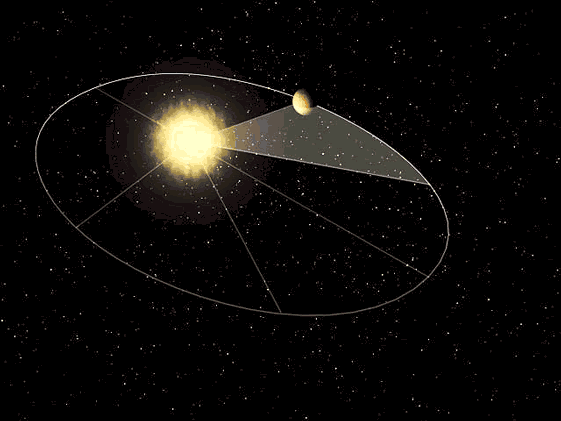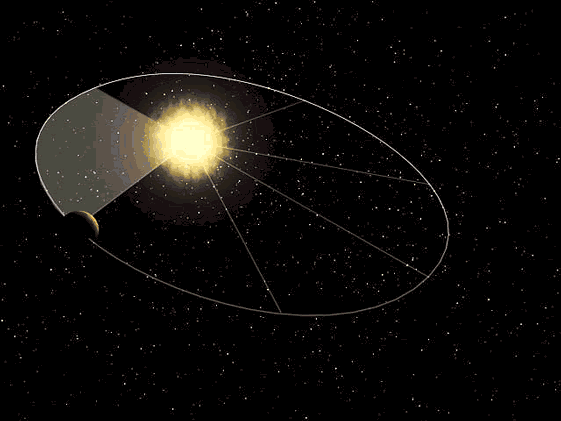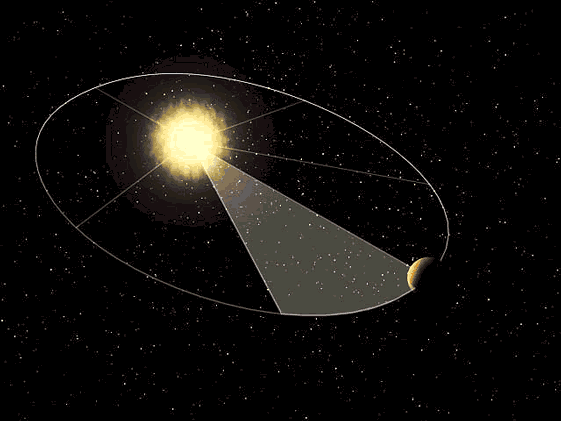
Второй закон Кеплера (http://2012god.ru/spasibo-kepleru/)

Следовательно, линейная скорость движения планеты неодинакова в разных точках ее орбиты. Скорость планеты при движении ее по орбите тем больше, чем ближе она к Солнцу. В перигелии скорость планеты наибольшая, в афелии наименьшая. Таким образом, второй закон Кеплера количественно определяет изменение скорости движения планеты по эллипсу.

Проверить это можно сравнив данные в таблице Солнечной системы.

3) Третий закон Кеплера. 

Мы наблюдаем планеты с Земли, которая сама обращается вокруг Солнца. Это движение Земли необходимо учитывать, чтобы узнать периоды обращения планет в невращающейся инерциальной системе отсчета, или, как часто говорят, по отношению к звездам.

Период обращения планет вокруг Солнца по отношению к звездам называется звездным или сидерическим периодом.

Чем ближе планета к Солнцу, тем больше ее линейная и угловая скорости и короче звездный период обращения вокруг Солнца.

Однако из непосредственных наблюдений определяют не сидерический период обращения планеты, а промежуток времени, протекающий между ее двумя последовательными одноименными конфигурациями, например между двумя последовательными соединениями (противостояниями). Этот период называется синодическим периодом обращения. Определив из наблюдений синодические периоды, путем вычислений находят звездные периоды обращения планет Т.

Рассмотрим, как же связаны синодический и звездный периоды обращения планет на примере Марса.

Скорость движения планет тем больше, чем они ближе к Солнцу. Поэтому после противостояния Марса Земля станет его обгонять. С каждым днем она будет отходить от него все дальше. Когда она обгонит его на полный оборот, то снова произойдет противостояние.

Синодический период внешней планеты - это промежуток времени, по истечении которого Земля обгоняет планету на 360° при их движении вокруг Солнца.

Сидерический период                                          Синодический период

Соотношение между сидерическим и синодическим периодами

Если S - синодический период планеты в сутках, то через S суток Земля, обгонит планету на 360°,

т. е.

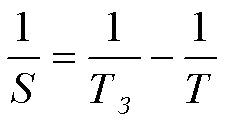
Для внутренних планет, обращающихся быстрее, чем Земля, Т>Т (планета будет обгонять Землю):

.

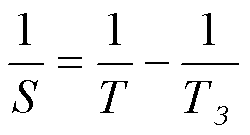Третий закон Кеплера: Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит.

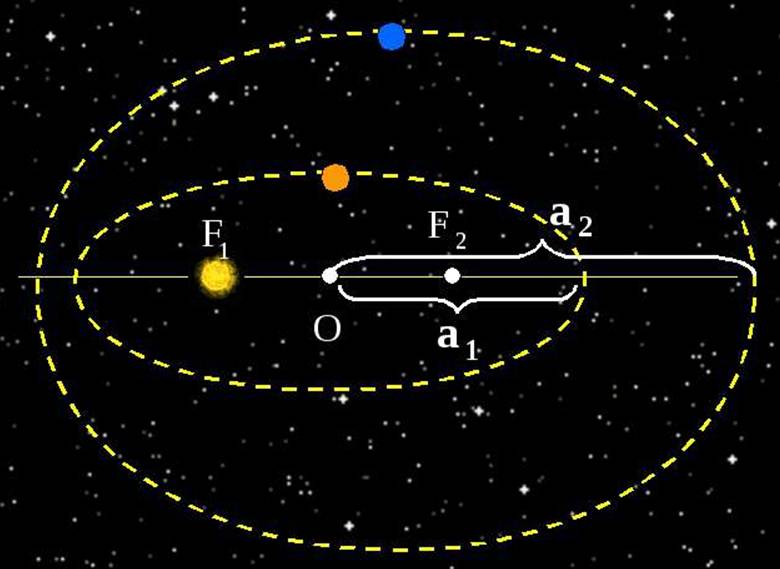
Если большую полуось орбиты и звездный период обращения одной планеты обозначить через a₁,T₁, а другой планеты - через а₂, Т₂, то формула третьего закона будет такова:

  .

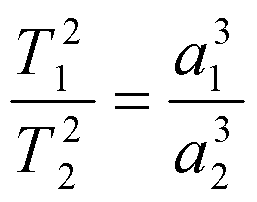Этот закон Кеплера связывает средние расстояния планет от Солнца с их звездными периодами и позволяет установить относительные расстояния планет, от Солнца, поскольку звездные периоды планет уже были вычислены, исходя из синодических периодов, иначе говоря, позволяет выразить большие полуоси всех планетных орбит в единицах большой полуоси земной орбиты.

Большая полуось земной орбиты принята за астрономическую единицу расстояний (а=1 а. е.).

Ее значение в километрах было определено позднее, лишь в XVIII в.

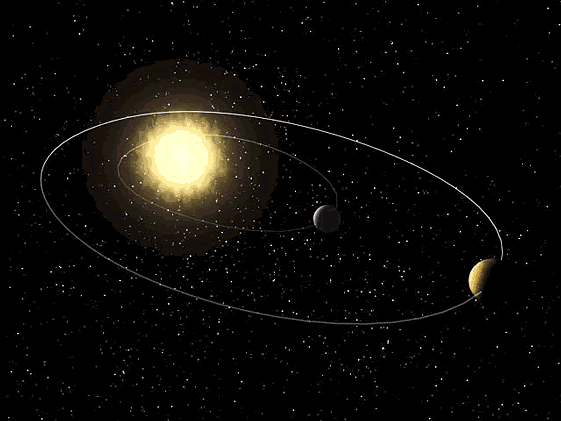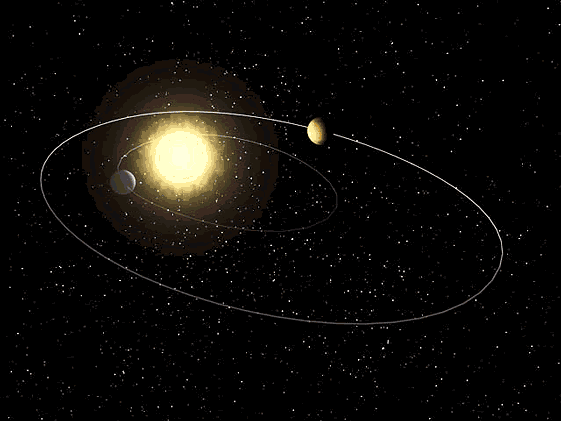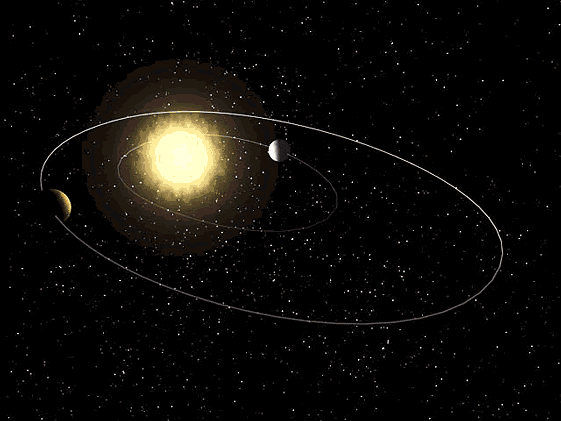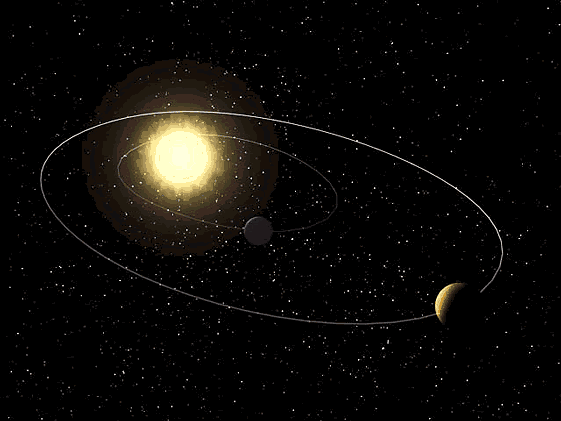
Третий закон Кеплера (http://2012god.ru/spasibo-kepleru/)

2. Космические скорости и форма орбит

Исходя из наблюдений движения Луны и анализируя законы движения планет, открытые Кеплером, И. Ньютон (1643-1727) установил закон всемирного тяготения. По этому закону, все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

,

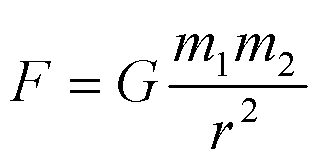здесь m₁ и m₂ - массы двух тел,

 r - расстояние между ними,

G - коэффициент пропорциональности, называемый гравитационной постоянной.

Закон всемирного тяготения объясняет движение планет и комет вокруг Солнца, движение спутников вокруг планет, двойных и кратных звезд вокруг их общего центра масс.

Ньютон доказал, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу (в частности, по кругу), по параболе и по гиперболе. Ньютон установил, что вид орбиты, которую описывает тело, зависит от его скорости в данном месте орбиты.

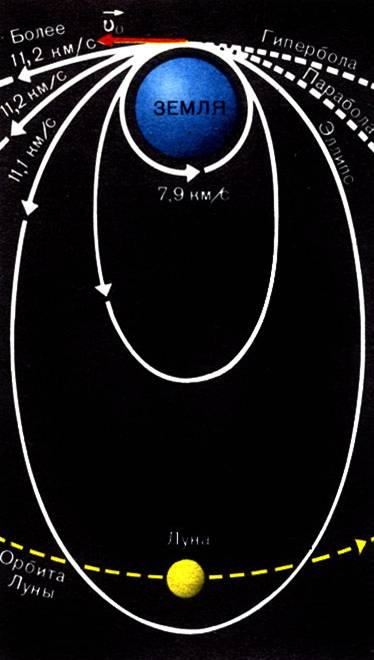
При некоторой скорости тело описывает окружность около притягивающего центра. Такую скорость называют первой космической или круговой скоростью, ее сообщают телам, запускаемым в качестве искусственных спутников Земли по круговым орбитам. Первая космическая скорость вблизи поверхности Земли составляет около 8 км/с (7,9 км/с).

Орбита спутника http://scientificstar.ru/photo/47-0-12823

Спутники вокруг Земли (http://www.variable-stars.ru/db/print/msg/1191583/earthsat_fu_big.gif.html)

Если телу сообщить скорость, большую круговой (11,2 км/с), называемую второй космической или параболической скоростью, то тело навсегда удалится от Земли и может стать спутником Солнца. В этом случае движение тела будет происходить по параболе относительно Земли.

При еще большей скорости относительно Земли тело полетит по гиперболе. Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.

3. Определение масс небесных тел

Ньютон доказал, что более точная формула третьего закона Кеплера такова:

 ,

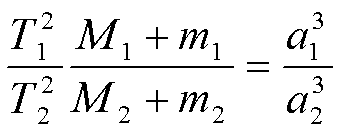где M₁ и М₂ - массы каких-либо небесных тел,

m₁ и m₂ - соответственно массы их спутников.

Так, планеты считаются спутниками Солнца. Мы видим, что уточненная формула этого закона отличается от приближенной наличием множителя, содержащего массы.

Если под M₁=M₂=M_С понимать массу Солнца, а под m₁ и m₂ - массы двух разных планет, то отношение

будет мало отличаться от единицы, так как m₁ и m₂ очень малы по сравнению с массой Солнца. При этом точная формула не будет заметно отличаться от приближенной.

Уточненный третий закон Кеплера позволяет определить массы планет, имеющих спутники, и массу Солнца. Чтобы определить массу Солнца, будем сравнивать движение Луны вокруг Земли с движением Земли вокруг Солнца:

,

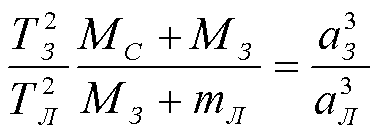где Т_З и а_З - период обращения Земли (год) и большая полуось ее орбиты,

T_Л и а_Л - период обращения Луны вокруг Земли и большая полуось ее орбиты, М - масса Солнца,

М_З - масса Земли, m_Л -масса Луны.

Масса Земли ничтожна по сравнению с массой Солнца, а масса Луны мала по сравнению с массой Земли. Поэтому вторые слагаемые в суммах можно отбросить, не делая большой ошибки.

Имеем:   

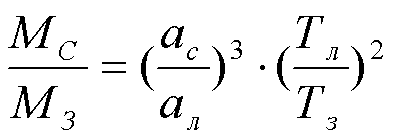
Эта формула позволяет определить массу Солнца, выраженную в массах Земли. Она составляет около 333 000 масс Земли.

Для сравнения масс Земли и другой планеты, например Юпитера, надо в исходной формуле индекс 1 отнести к движению Луны вокруг Земли массой M₁, a 2 - к движению любого спутника вокруг Юпитера массой М₂.

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они своим притяжением производят в движении соседних с ними планет, а также в движении комет, астероидов или космических аппаратов.

Задачи.

1. Звездный период обращения Юпитера равен 12 годам. Через какой промежуток времени повторяются его противостояния?

Дано:                                 

Т_з =1 год                            

 Т_Ю =12 лет                              

а_з = 1 а.е             

  Решение:

Звездный период найдем из соотношения между сидерическим и синодическим периодами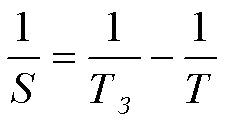.  S = 1,09 лет.

1 год- 365,25 сут

1,09 лет –х сут,   х = 1,09*365,25=398,45 сут       

Ответ: 398,45 сут  

2. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?

3. Синодический период обращения воображаемой планеты составляет 3 года. Каков звездный период ее обращения около Солнца?

4. Марс дальше от Солнца, чем Земля, в 1,5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Решение:

Из условия задачи получим, что большая полуось орбиты Марса a₂=1,5a=1,5 а.е. Тогда из третьего закона Кеплера, приняв для Земли a₁ =1 а.е. и T₁ =1 год, получим для Марса: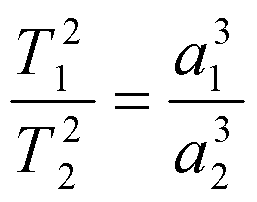               Т₂ ² = a₂ ³       T₂ =a ^3/2  =1,8 года

Ответ: 1,8 года

5. Синодический период малой планеты 500 сут. Определите большую полуось ее орбита и звездный период обращения.

6. Определите массу Юпитера сравнением системы Юпитера со спутником с системой Земля - Луна, если первый спутник Юпитера отстоит от него на 422 000 км и имеет период обращения 1,77 сут. Данные для Луны должны быть вам известны.

Дано:

Земля: M_З= 1 T_З = 27,32сут a_З= 3.84⋅10⁵км

Юпитер спутник И:  T_И =1,77 сут    а_И = 4,2⋅10⁵км

Решение: Обобщенный третий закон Кеплера: , пренебрегая массой спутников получаем: .

М_Ю = 317 масс Земли.

Ответ:  Масса Юпитера составляет примерно 317 масс Земли.

7. Вычислите, на каком расстоянии от Земли на линии Земля - Луна находятся те точки, в которых притяжения Землей и Луной одинаковы, зная, что расстояние между Луной и Землей равно 60 радиусам Земли, а масса Земли в 81 раз больше массы Луны

Контрольные вопросы:

1. Сформулируйте первый закон Кеплера

2. Сформулируйте второй закон Кеплера

3. Сформулируйте третий закон Кеплера

4. Запишите соотношение между сидерическим и синодическим периодами для внутренних планет.

5. Запишите соотношение между сидерическим и синодическим периодами для внешних планет.

6. Что называется сидерическим периодом?

7. Что называется синодическим периодом?

8. Что называется перигеем?

9. Какой закон Кеплера количественно определяет изменение скорости движения планеты по эллипсу

10. Какой закон Кеплера связывает средние расстояния планет от Солнца с их звездными периодами и позволяет установить относительные расстояния планет от Солнца.

11. По каким орбитам движется тело вокруг Земли, запущенное в космос с первой, второй, третьей космическими скоростями?

Домашнее задание:

1. Какова должна быть продолжительность звездного и синодического периодов обращения планеты в случае их равенства?

2. Как часто повторяются противостояния планеты (Сатурна), сидерический период которой известен.

3. Вычислить массу планеты (Уран), зная сидерический период обращения ее спутника (Миранда) и расстояние спутника от планеты.

Задание:
Подготовить презентацию «Планеты Солнечной системы» по одной из тем:
1. Происхождение солнечной вселенной
2. Планета Марс
3. Связь Луны с приливами и отливами на Земле
4. Фазы Луны
5, Планеты Венера
6. Планета Меркурий
7. Планета Земля
8. Планета Юпитер
9. Планета Уран
10. Планета Сатурн
11. Планета Нептун
12. Кольца и Спутники
13. Астероиды
14. Физическая природа комет
15. Метеориты
 

Методические рекомендации
Подготавливая презентацию о планете, придерживайтесь такого плана:
1. Группа, к которой принадлежит планета. Отличительные характеристики данной группы.
2. Размеры и масса планеты.
3. Расстояние планеты от Солнца.
4. Периоды ее вращения и обращения. Ось вращения.
5. Структура
6. Характеристика атмосферы.
7. Температурные условия.
8. Рельеф (для планет земной группы)
9. Магнитное поле планеты
10. Число и характеристика спутников
11. Характеристика колец (для планет гигантов)
При подготовке презентации об астероидах, кометах, метеоритах необходимо дать характеристику данному космическому телу, указать его возможные размеры, виды, отразить характер его перемещения в космосе, отметь наличие или отсутствие атмосферы.